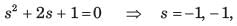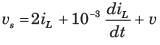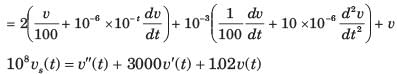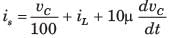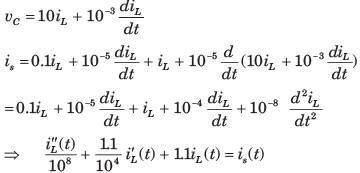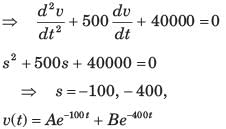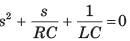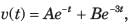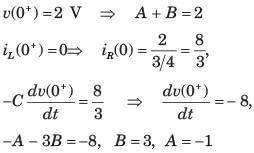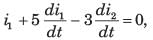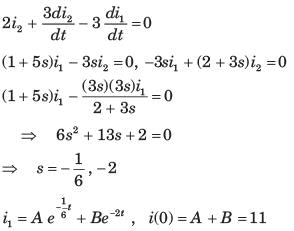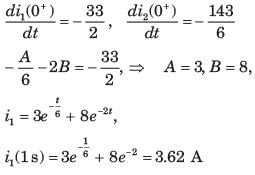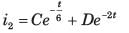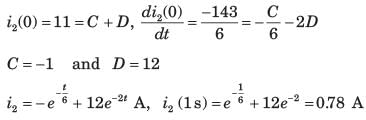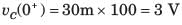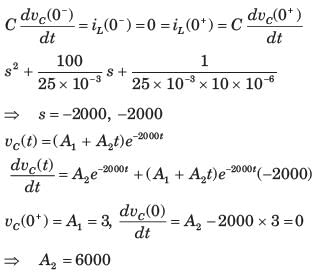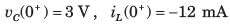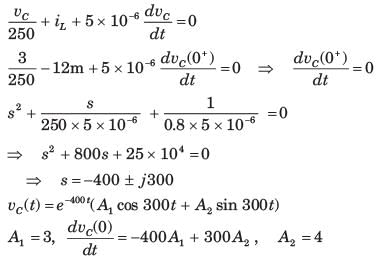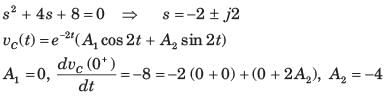Electrical Engineering (EE) Exam > Electrical Engineering (EE) Tests > Test: Transient Response of DC & AC Networks - 1 - Electrical Engineering (EE) MCQ
Test: Transient Response of DC & AC Networks - 1 - Electrical Engineering (EE) MCQ
Test Description
10 Questions MCQ Test - Test: Transient Response of DC & AC Networks - 1
Test: Transient Response of DC & AC Networks - 1 for Electrical Engineering (EE) 2024 is part of Electrical Engineering (EE) preparation. The Test: Transient Response of DC & AC Networks - 1 questions and answers have been prepared
according to the Electrical Engineering (EE) exam syllabus.The Test: Transient Response of DC & AC Networks - 1 MCQs are made for Electrical Engineering (EE) 2024 Exam.
Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Transient Response of DC & AC Networks - 1 below.
Solutions of Test: Transient Response of DC & AC Networks - 1 questions in English are available as part of our course for Electrical Engineering (EE) & Test: Transient Response of DC & AC Networks - 1 solutions in
Hindi for Electrical Engineering (EE) course.
Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free. Attempt Test: Transient Response of DC & AC Networks - 1 | 10 questions in 30 minutes | Mock test for Electrical Engineering (EE) preparation | Free important questions MCQ to study for Electrical Engineering (EE) Exam | Download free PDF with solutions
Test: Transient Response of DC & AC Networks - 1 - Question 1
The natural response of an RLC circuit is described by the differential equation
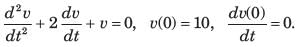
The v(t) is
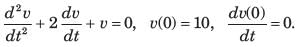
The v(t) is
Detailed Solution for Test: Transient Response of DC & AC Networks - 1 - Question 1
Test: Transient Response of DC & AC Networks - 1 - Question 2
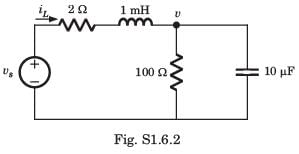
The differential equation for the circuit shown in fig. P1.6.2. is
Detailed Solution for Test: Transient Response of DC & AC Networks - 1 - Question 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Test: Transient Response of DC & AC Networks - 1 - Question 3
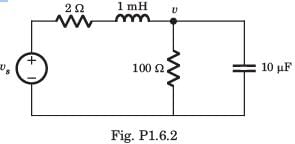
The differential equation for the circuit shown in fig. P1.6.3 is
Detailed Solution for Test: Transient Response of DC & AC Networks - 1 - Question 3
Test: Transient Response of DC & AC Networks - 1 - Question 4
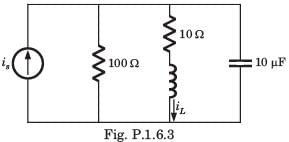
In the circuit of fig. P.1.6.4 vs = 0 for t > 0. The initial condition are v(0) = 6 V and dv(0) dt = -3000 Vs. The v(t) for t > 0 is
Detailed Solution for Test: Transient Response of DC & AC Networks - 1 - Question 4
Test: Transient Response of DC & AC Networks - 1 - Question 5
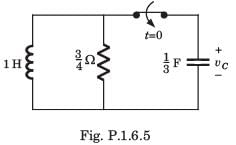
The circuit shown in fig. P1.6.5 has been open for a long time before closing at t = 0. The initial condition is v(0) = 2 V. The v(t) for t > is
Detailed Solution for Test: Transient Response of DC & AC Networks - 1 - Question 5
Test: Transient Response of DC & AC Networks - 1 - Question 6
Circuit is shown in fig. P.1.6. Initial conditions are i1(0) = i2(0) = 11A
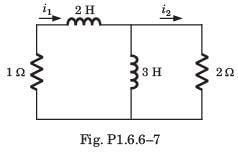
Q. i1 (1 s) = ?
Detailed Solution for Test: Transient Response of DC & AC Networks - 1 - Question 6
Test: Transient Response of DC & AC Networks - 1 - Question 7
Circuit is shown in fig. P.1.6. Initial conditions are i1(0) = i2(0) = 11A
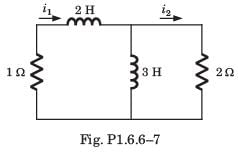
Q. i2 (1 s) = ?
Detailed Solution for Test: Transient Response of DC & AC Networks - 1 - Question 7
Detailed Solution for Test: Transient Response of DC & AC Networks - 1 - Question 8
Test: Transient Response of DC & AC Networks - 1 - Question 9
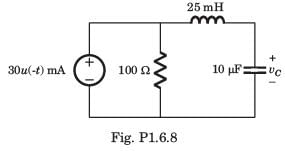
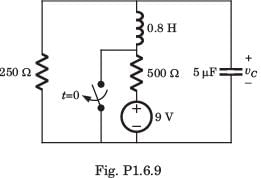
The circuit shown in fig. P1.6.9 is in steady state with switch open. At t = 0 the switch is closed. The output voltage vC(t) for t > 0 is
Detailed Solution for Test: Transient Response of DC & AC Networks - 1 - Question 9
Test: Transient Response of DC & AC Networks - 1 - Question 10
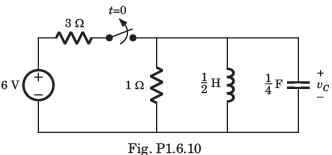
The switch of the circuit shown in fig. P1.6.10 is opened at t = 0 after long time. The v(t) , for t > 0 is
Detailed Solution for Test: Transient Response of DC & AC Networks - 1 - Question 10
Information about Test: Transient Response of DC & AC Networks - 1 Page
In this test you can find the Exam questions for Test: Transient Response of DC & AC Networks - 1 solved & explained in the simplest way possible.
Besides giving Questions and answers for Test: Transient Response of DC & AC Networks - 1, EduRev gives you an ample number of Online tests for practice
Download as PDF
Top Courses for Electrical Engineering (EE)
Important Questions for Transient Response of DC & AC Networks - 1
Find all the important questions for Transient Response of DC & AC Networks - 1 at EduRev.Get fully prepared for Transient Response of DC & AC Networks - 1 with EduRev's comprehensive question bank and test resources.
Our platform offers a diverse range of question papers covering various topics within the Transient Response of DC & AC Networks - 1 syllabus.
Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered.
The questions are designed to challenge you and help you gain confidence in tackling the actual exam.
Maximize your chances of success by utilizing EduRev's extensive collection of Transient Response of DC & AC Networks - 1 resources.
Transient Response of DC & AC Networks - 1 MCQs with Answers
Prepare for the Transient Response of DC & AC Networks - 1 within the Electrical Engineering (EE) exam with comprehensive MCQs and answers at EduRev.
Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus.
Access the best books, study materials, and notes curated by toppers to enhance your preparation.
Stay updated with the exam date and receive expert preparation tips and paper analysis.
Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.
Online Tests for Transient Response of DC & AC Networks - 1
Practice with a wide array of question papers that follow the exam pattern and syllabus.
Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement.
Access detailed solutions and explanations for each test to enhance your understanding of concepts.
With EduRev's Online Tests, you can build confidence, boost your performance, and ace Transient Response of DC & AC Networks - 1 with ease.
Join thousands of successful students who have benefited from our trusted online resources.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup