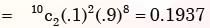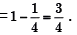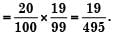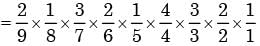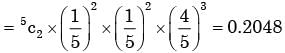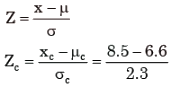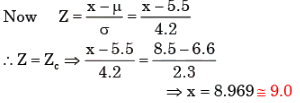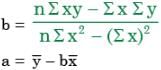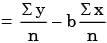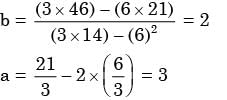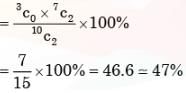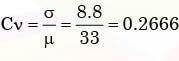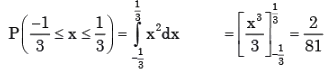Test: Probability Part:- 2 - Mathematics MCQ
20 Questions MCQ Test - Test: Probability Part:- 2
A lot has 10% defective items. Ten items are chosen randomly from this lot. The probability that exactly 2 of the chosen items are defective is
A single die is thrown twice. What is the sum is neither 8 nor 9?
A box contains 20 defective items and 80 non-defective items. If two items are selected at random without replacement, what will be the probability that both items are defective?
A coin is tossed 4 times. What is the probability of getting heads exactly 3 times?
If three coins are tossed simultaneously, the probability of getting at least one head is
A box contains 2 washers, 3 nuts and 4 bolts. Items are drawn from the box at random one at a time without replacement. The probability of drawing 2 washers first followed by 3 nuts and subsequently the 4 bolts is
If 20 per cent managers are technocrats, the probability that a random committee of 5 managers consists of exactly 2 technocrats is
Four arbitrary point (x1,y1), (x2,y2),(x3,y3), (x4,y4), are given in the x, y - Plane Using the method of least squares, if, regressing y upon x gives the fitted line y = ax + b; and regressing y upon x given the fitted line x = cy + d then
A regression model is used to express a variable Y as a function of another variable X. This implies that
Let X and Y be two independent random variables. Which one of the relations between expectation (E), variance (Var) and covariance (Cov) given below is FALSE?
A class of first year B. Tech. Students is composed of four batches A, B, C and D, each consisting of 30 students. It is found that the sessional marks of students in Engineering Drawing in batch C have a mean of 6.6 and standard deviation of 2.3. The mean and standard deviation of the marks for the entire class are 5.5 and 4.2, respectively. It is decided by the course instructor to normalize the marks of the students of all batches to have the same mean and standard deviation as that of the entire class. Due to this, the marks of a student in batch C are changed from 8.5 to
Three values of x and y are to be fitted in a straight line in the form y = a + bx by the method of least squares. Given ∑x = 6, ∑y = 21, ∑x2 = 14 and ∑xy = 46, the values of a and b are respectively.
A box contains 10 screws, 3 of which are defective. Two screws are drawn at random with replacement. The probability that none of the two screws is defective will be
A hydraulic structure has four gates which operate independently. The probability of failure off each gate is 0.2. Given that gate 1 has failed, the probability that both gates 2 and 3 will fail is
There are 25 calculators in a box. Two of them are defective. Suppose 5 calculators are randomly picked for inspection (i.e., each has the same chance of being selected), what is the probability that only one of the defective calculators will be included in the inspection?
If the standard deviation of the spot speed of vehicles in a highway is 8.8 kmph and the mean speed of the vehicles is 33 kmph, the coefficient of variation in speed is
If probability density functions of a random variable X is f(x) = x2 for -1 ≤ x ≤ 1, and = for any other value of x
Then, the percentage probability 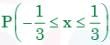 is
is
A person on a trip has a choice between private car and public transport. The probability of using a private car is 0.45. While using the public transport, further choices available are bus and metro, out of which the probability of commuting by a bus is 0.55. In such a situation, the probability (rounded up to two decimals) of using a car, bus and metro, respectively would be