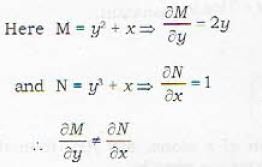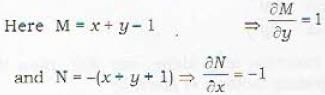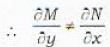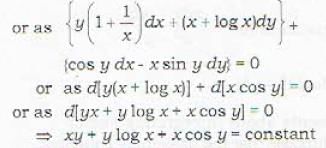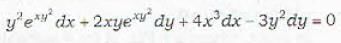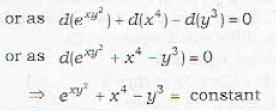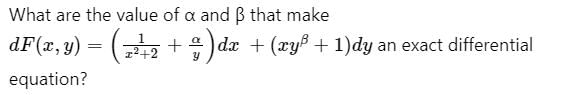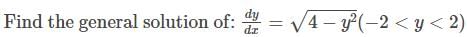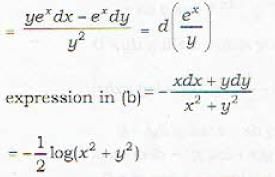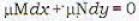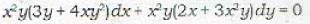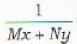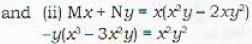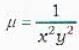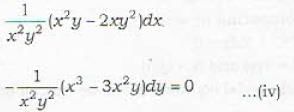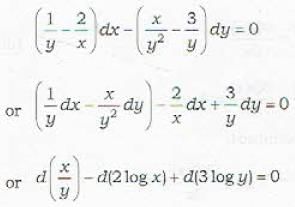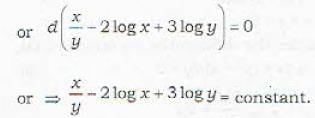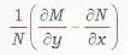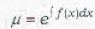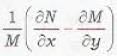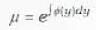Differential Equations - 16 - Mathematics MCQ
20 Questions MCQ Test - Differential Equations - 16
The differential equation of all circles of radius a is given by
Which of the following differential equations is linear?
Which of the following differential equations is linear but not of first degree
Which one of the following is a standard form of the first order differential equation of first degree?
If M and N are functions of x and y, then the equation Mdx + Ndy = 0 is exact if
The necessary and sufficient condition for the differential equation M(x, y)dx + N(x, y)dy = 0 to be exact is that
If P(x) and Q(y) are arbitrary functions of x and y respectively, then the differential equation P(x)dx + Q(y)dy = 0
If P(y) and Q(x) are arbitrary functions of y and a respectively, then the differential equation P(y)dx+ Q(x)dy = 0
Which of the following differential equation is exact?
Which of the following differential equations is exact?
Which of the following provides a solution of the exact differential equation
 + {x + log x - x sin y}dy = 0
+ {x + log x - x sin y}dy = 0
Which of the following provides a solution of the exact differential equation 
The integrating factor of the differential equation xdx - ydx = xy2dx is



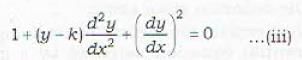
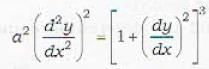

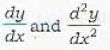
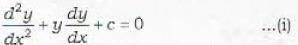


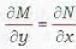
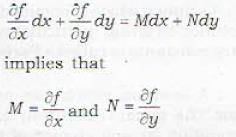
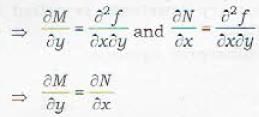
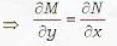
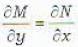
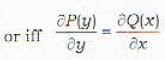 ...(iii)
...(iii)