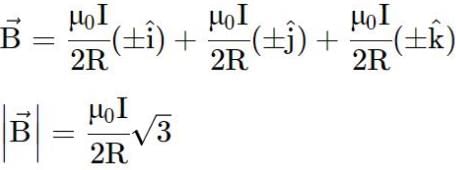Test: Magnetism & Matter - 3 - JEE MCQ
27 Questions MCQ Test - Test: Magnetism & Matter - 3
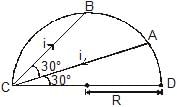
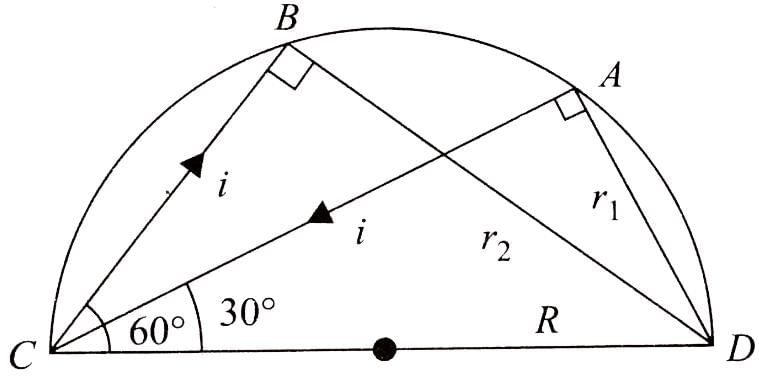
A current carrying wire is placed in the grooves of an insulating semi circular disc of radius `R', as shown. The current enters at point A and leaves from point B. Determine the magnetic field at point D.
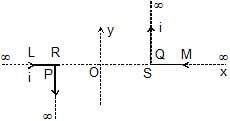
A pair of stationary and infinitely long bent wires is placed in the X-Y plane as shown in figure. The wires carry currents of 10 A each as shown. The segments L and M are along thex-axis. The segments P and Q are parallel to the y-axis such that OS = OR = 0.02 m. Find the magnetic induction at the origin O.
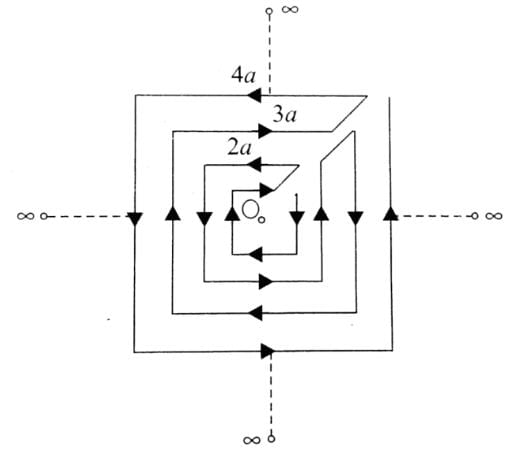
Determine the magniutde of magnetic field at the centre of the current carrying wire arrangement shown in the figure. The arrangement extends to infinity. (The wires joining the successive square are along the line passing through the centre)

Figures shows a long wire bent at the middle to form a right angle. The magnitudes of the magnetic fields at the points P, Q, R and S are B1, B2, B3, B4respectively. The wire and the circumference of circle are coplaner. T
Two long parallel wires situated at a distance 2a are carrying equal current `i' in opposite direction as shown in figure. The value of magnetic field at a point P situated at equal distances from both the wires will be :
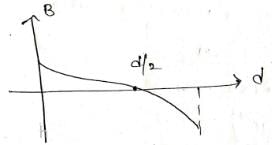
A uniform beam of positively charged particles is moving with a constant velocity parallel to another beam of negatively charged particles moving with the same velocity in opposite direction separated by a distance d. The variation of magnetic field B along a perpendicular line draw between the two beams is best represented by
Infinite number of straight wires each carrying current I are equally placed as shown in the figure. Adjacent wires have current in opposite direction. Net magnetic field at point P is
Two mutually perpendicular conductors carrying currents I1 and I2 lie in one plane. Locus of the point at which the magnetic induction is zero, is a
Consider the magnetic field produced by a finitely long current carrying wire.
Consider three quantities x =E/B, y = and z =
. Here, l is the length of a wire, C is a capacitance and R is a resistance. All other symbols have standard meanings.
Two long thin, parallel conductors carrying equal currents in the same direction are fixed parallel to the x–axis, one passing through y = a and the other through y = –a. The resultant magnetic field due to the two conductors at any point is B. Which of the following are correct ?
Current flows through uniform, square frames as shown. In which case is the magnetic field at the centre of the frame not zero ?
The two conductors of a transmission line carry equal current I in opposite directions. The force on each conductor is
In the previous question, if the current is i and the magnetic field at D has magnitude B,
Three rings, each having equal radius R, are placed mutually perpendicular to each other and each having its centre at the origin of co-ordinate system. If current I is flowing through each ring then the magnitude of the magnetic field at the common centre is
Two concentric coils X and Y of radii 16 cm and 10 cm lie in the same vertical plane containing N-S direction. X has 20 turns and carries 16 A. Y has 25 turns & carries 18 A. X has current in anticlockwise direction and Y has current in clockwise direction for an observer, looking at the coils facing the west. The magnitude of net magnetic field at their common centre is
A current i is passed through a silver strip of width d and area of cross-section A. The number of free electrons per unit volume is n.
Find the drift velocity v of the electrons.
A current i is passed through a silver strip of width d and area of cross-section A. The number of free electrons per unit volume is n.
If a magnetic field B exists in the region as shown in figure, what is the average magnetic force on the free electrons ?
A current i is passed through a silver strip of width d and area of cross-section A. The number of free electrons per unit volume is n.
Due to the magnetic force, the free electrons get accumulated on one side of the conductor along its length. This produces a transverse electric field in the conductor which opposes the magnetic force on the electrons. Find the magnitude of the electric field which will stop further accumulation of electrons.
A current i is passed through a silver strip of width d and area of cross-section A. The number of free electrons per unit volume is n.
What will be the potential difference developed across the width of the conductor due to the electron accumulation ? The appearance of a transverse emf, when a current - carrying wire is placed in a magnetic field, is called Hall effect.
Six wires of current I1 = 1 A, I2 = 2A, I3 = 3A, I4 = 1A, I5 = 5A and I6 = 4A cut the page perpendicularly at the points 1,2,3,4,5 and 6 respectively as shown in the figure. Find the value of the integral around the closed path.
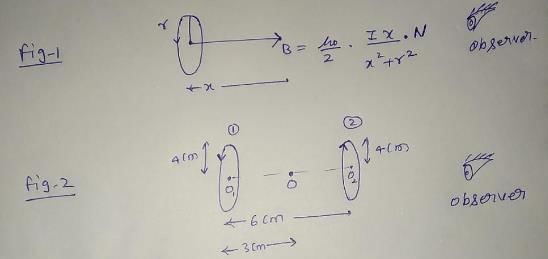
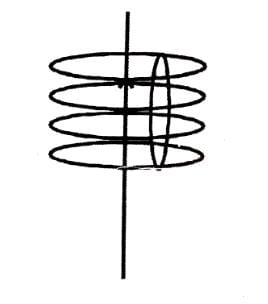
Two circular coils of wire each having a radius of 4 cm and 10 turns have a common axis and are 6 cm apart. If a current of 1 A passes through each coil in the opposite direction find the magnetic induction.
Q.
At the centre of either coil
Two circular coils of wire each having a radius of 4 cm and 10 turns have a common axis and are 6 cm apart. If a current of 1 A passes through each coil in the opposite direction find the magnetic induction.
Q.
At a point on the axis, midway between them.
Find the ratio of magnetic field magnitudes at a distance 10 m along the axis and at 60° from the axis, from the centre of a coil of radius 1 cm, carrying a current 1 amp.
A particle of charge +q and mass m moving under the influence of a uniform electric field E and a magnetic field B enters in I quadrant of a coordinate system at a point (0, a) with initial velocity v
and leaves the quadrant at a point (2a, 0) with velocity - 2v . Find
Magnitude of electric field
A particle of charge +q and mass m moving under the influence of a uniform electric field E and a magnetic field B enters in I quadrant of a coordinate system at a point (0, a) with initial velocity v
and leaves the quadrant at a point (2a, 0) with velocity - 2v . Find
Rate of work done by the electric field at point (0, a)
A particle of charge +q and mass m moving under the influence of a uniform electric field E and a magnetic field B enters in I quadrant of a coordinate system at a point (0, a) with initial velocity v
and leaves the quadrant at a point (2a, 0) with velocity - 2v . Find
Rate of work done by both the fields at (2a, 0)


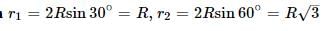
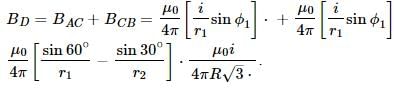


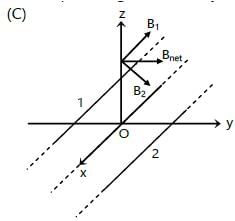 B cannot have x-component as B is perpendicular to direction of I.
B cannot have x-component as B is perpendicular to direction of I.