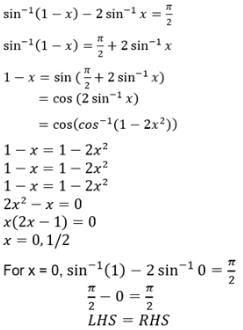JEE Advanced Level Test: Inverse Trigonometry- 2 - Airforce X Y / Indian Navy SSR MCQ
28 Questions MCQ Test - JEE Advanced Level Test: Inverse Trigonometry- 2
Domain of f(x) = cos–1 x + cot–1 x + cosec–1 x is
Range of f(x) = sin–1 x + tan–1 x + sec–1 x is
If ƒ(x) = tan(x), then f-1(1/√(3)) =
If cos [tan-1 {sin(cot-1 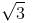 )}] = y, then :
)}] = y, then :
The value of x for which sin [cot–1(1+x)] = cos(tan–1x)
If 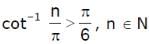 , then the maximum value of 'n' is
, then the maximum value of 'n' is
The value of sin–1 (sin 12) + cos–1 (cos 12) is equal to
The value of sin-1[cos{cos-1 (cos x) + sin-1(sin x)}], where x
Which of the following is different from 2tan−1x?
If x< 0 then value of tan-1(x) + tan-1 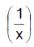 is equal to
is equal to
tan–1 a + tan–1b, where a > 0, b > 0, ab > 1, is equal to
The smallest and the largest values of 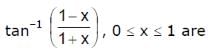
The principal value of cos–1 (cos 5) is
The value of sin–1 (sin 12) + cos–1 (cos 12) is equal to
Which one of the following correct ?
The equation sin-1 x - cos-1 x =  has
has
The set of values of ‘x’ for which the formula 2 sin-1 x = sin-1 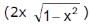 is true is
is true is
The value of x satisfying sin–1 x + sin–1(1 – x) = cos–1 x are
The number of solutions of the equation tan-1(1 + x) + tan-1(1 – x) = π/2 is
The number of solution(s) of the equation Sin-1(1 – x) – 2sin-1 x = π/2 , is / are
The number of solutions of the equation 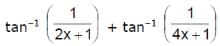
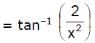 is
is



 is
is 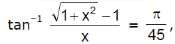 then
then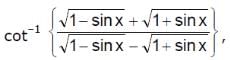
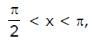 is
is 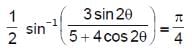 , then tan θ is equal to
, then tan θ is equal to  , then a value of x is
, then a value of x is