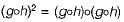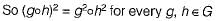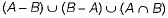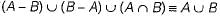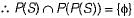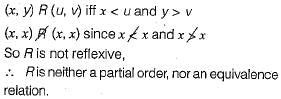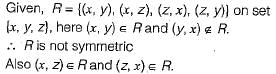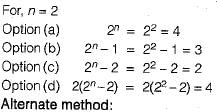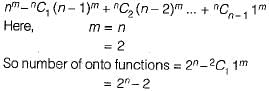Test: Set Theory & Algebra- 2 - Computer Science Engineering (CSE) MCQ
15 Questions MCQ Test - Test: Set Theory & Algebra- 2
Some group (G, o) is known to be abelian. Then, which one of the following is true for G?
Let R be a sym m etric and transitive relation on a set A Then
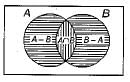
Let A and B be sets and let Ac and Bc denote the complements of the sets A and B. The set (A - B) ∪ (B - A) ∪ (A ∩ B) is equal to
The binary relation R = {(1, 1), (2, 1), (2, 2), (2, 3), (2, 4), (3, 1), (3, 2), (3, 3), (3, 4)},on the set A = {1 , 2 , 3, 4} is
Let' P(S) denote the power set of a set S. Which of the following is always true?
Consider the set ∑* of all strings over the alphabet ∑ = {0,1}. ∑* with the concatenation operator for strings
Consider the binary relation:
S = {(x, y) | y = x + 1 and x, y ∈ {0, 1, 2, ...}}
The reflexive transitive closure of S is
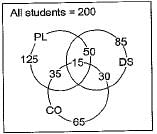
In a class of 200 students, 125 students have taken Programming Language course, 85 students have taken Data Structures course, 65 students have taken Computer Organization course; 50 students have taken both Programming Language and Data Structures, 35 students have taken both Data Structures and Computer Organization; 30 students have taken both Data Structures and Computer Organization, 15 students have taken all the three courses. How many students have not taken any of the three courses?
Let A, B and C be non-empty sets and let X = (A - B ) -C and Y = (A - C) - (B - C) Which one of the following is TRUE?
The set {1, 2, 4, 7, 8,11,13,14} is a group under multiplication modulo 15. The inverses of 4 and 7 are respectively
A relation R fs defined on ordered pairs of integers as follows: (x, y) R (u, v) if x < u and y > v. Then R is
Let P, Q and R be sets let A denote the symmetric difference operator defined as PΔG = ( P ∪ Q) - (P ∩ Q). Using Venn diagrams, determine which of the following is/are TRUE?
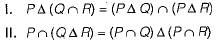
Consider the binary relation: R = {(x, y), (x, z), (z, x), (z, y)} on the set {x, y, z}. Which one of the following is TRUE?
How many onto (or surjective) functions are there from an n-element (n ≥ 2) set to a 2-element set?