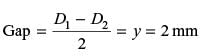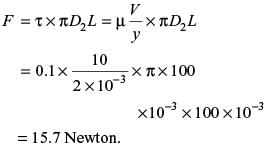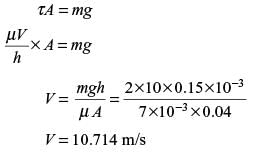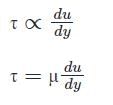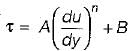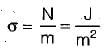Test: Properties of Fluids - 2 - Mechanical Engineering MCQ
15 Questions MCQ Test - Test: Properties of Fluids - 2
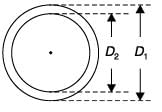
In a simple concentric shaft-bearing arrangement, the lubricant flows in the 2 mm gap between the shaft and the bearing. The flow may be assumed to be a plane couette flow with zero pressure gradients. The diameter of the shaft is 100 mm and its tangential speed is 10 m/s. The dynamic viscosity of the lubricant is 0.1 kg/m ∙ s. The frictional resisting force (in Newton) per 100 mm length of the bearing is _____(Give answer about 1 decimal place)
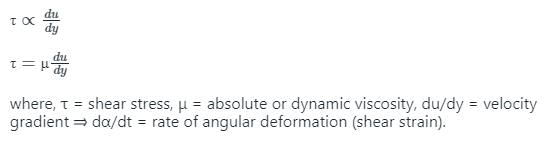
Newton’s law of viscosity for a fluid states that the shear stress is
A flat plate of width L = 1 m is pushed down with a velocity U = 0.01 m/s towards a wall resulting in the drainage of the fluid between the plate and the wall as shown in the figure. Assume two-dimensional incompressible flow and that the plate remains parallel to the wall. The average velocity, Uavg of the fluid (in m/s) draining out at the instant shown in the figure is _______ (correct to three decimal places).


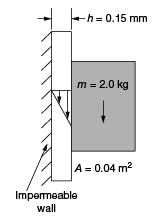
A solid block of 2.0 kg mass slides steadily at a velocity V along a vertical wall as shown in the figure below. A thin oil film of thickness h = 0.15 mm provides lubrication between the block and the wall. The surface area of the face of the block in contact with the oil film is 0.04 m2. The velocity distribution within the oil film gap is linear as shown in the figure. Take dynamic viscosity of oil as 7.10–3 Pa-s and acceleration due to gravity as 10 ms2. Neglect weight of the oil. The terminal velocity V(in m s) of the block is ______ (correct to one decimal place).
Which one of the following is defined as force per unit length?
In incompressible fluid (kinematic viscosity = 7.4 × 10−7 m2/s, specific gravity, 0.88) is held between two parallel plates. If the top plate is moved with a velocity of 0.5 m/s while the bottom one is held stationary, the fluid attains a linear velocity profile in the gap of 0.5 mm between these plates; the shear stress in Pascal on the surface of bottom plate is
The fluid which obey’s the Newton’s law of viscosity 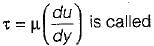
The General relationship between shear stress (τ) and velocity Gradient 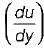 for a fluid can be written as
for a fluid can be written as
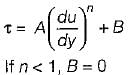
Then the fluid known as
Which one of the following is correct dimension of surface tension?
Kinematic viscosity of air at 20°C is given to be 1.6 × 10−5 m2/s. Its kinematic viscosity at 70°C will be varying approximately