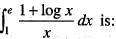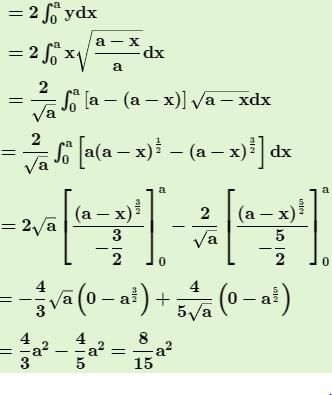Integral Calculus -4 - Mathematics MCQ
20 Questions MCQ Test - Integral Calculus -4
The length of the arc of the curve p = f (r) between the points r = a and r = b is given by:
The intrinsic equation of the cycloid x = a (θ + sin θ) , and y = a (1 - cos θ) is given by:
The volume of the tetrahedron bounded by the plane 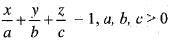 and the co-ordinate planes is equal to
and the co-ordinate planes is equal to
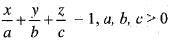 and the co-ordinate planes is equal to
and the co-ordinate planes is equal toThe volume of the cylinder x2 + y2 = a2 bounded below by z = 0 and bounded above by z = h is given by:
The volume bounded by the curve y = f( x ), x -axis and lines x = a, x = b is revolved about the x -axis , then the volume generated is:
What is the volume generated when the region surrounded by y = √x, y = 2 and y = 0 is revolved about y – axis?
The area included between the cycloid x = a(θ - sinθ) , y = a(1 - cosθ) and its base is:
The volume of the real formed by revolving part of the parabola y2 = 4ax cut off by the latus rectum about the tangent at the vertex is given by:
What is the formula used to find the area surrounded by the curves in the following diagram?
The area bounded by the curve 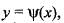 x-axis and the lines x = l, x = m (l < m) is given by:
x-axis and the lines x = l, x = m (l < m) is given by:
Let f(x) be bounded and integrable on [a , b] and let F(x) 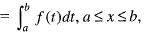 then
then


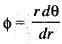
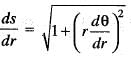
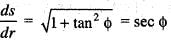

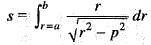
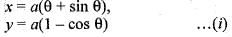
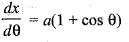
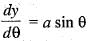 ...(ii)
...(ii)
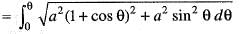
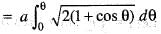
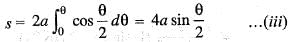
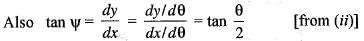
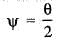
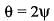


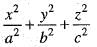 = 1 is:
= 1 is:

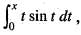 then f'(x) is equal to:
then f'(x) is equal to: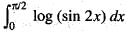 has the value:
has the value: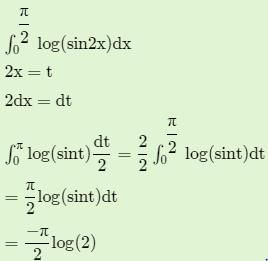
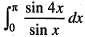 is equal to:
is equal to: 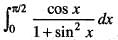 is equal to:
is equal to: