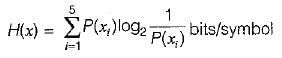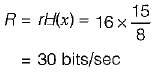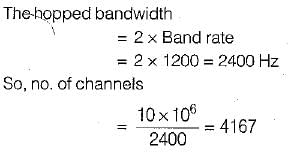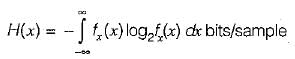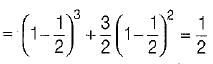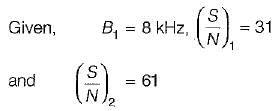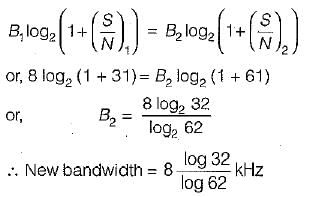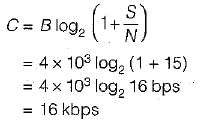Test: Information Theory & Coding - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Information Theory & Coding
The probabilities of the five possible outcomes of an experiment are given as:

If there are 16 outcomes per second then the rate of information would be equal to

Consider the binary Hamming code of block length 31 and rate equal to (26/31). Its minimum distance is
Assertion (A): The Shannon-Hartley law shows that we can exchange increased bandwidth for decreased signal power for a system with given capacity C.
Reason (R): The bandwidth and the signal power place a restriction upon the rate of information that can be transmitted by a channel.
Reason (R): The bandwidth and the signal power place a restriction upon the rate of information that can be transmitted by a channel.
A 1200 band data stream is to be sent over a non-redundant frequency hopping system, The maximum bandwidth for the spread spectrum signal is 10 MHz. if no overlap occurs, the number of channels are equal to
The differential entropy H(x) of the uniformly distributed random variable* with the following probability density function for a = 1 is

During transmission over a communication channel bit errors occurs independently with probability 1/2 . If a block of 3 bits are transmitted the probability of at least one bit error is equal to
A channel has a bandwidth of 8 kHz and signal to noise ratio of 31. For same channel capacity, if the signal to noise ratio is increased to 61, then, the new channel bandwidth would be equal to
A source generates 4 messages. The entropy of the source will be maximum when
A source delivers symbols m1, m2, m3 and m4 with probabilities 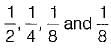 respectively.
respectively.
The entropy of the system is
A communication channel with AWGN has a BW of 4 kHz and an SNR pf 15. Its channel capacity is