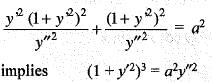Differential Equations - 2 - IIT JAM MCQ
20 Questions MCQ Test - Differential Equations - 2
Consider the differential equation y" + 6y' + 25y - 0 with initial condition y(0) = 0. Then, the general solution of the IVP is
What is the general solution of the differential equation y'' + 4y =0?
General solution of the differential equation 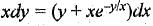 is given by
is given by
The orthogonal trajectories of the curves y2 = 3x3+x + c are
The solution of the initial value problem xy' - y = 0 with y(1) = 1 is
If y'1 (x) = 3y1(x) + 4y2(x) and y'2 (x) = 4y1(x) + 3y2(x), then y1(x) is
If ex + xy + x sin y + ey = c is the general solution of an exact differential equation, then the differential equation is
The differential equation (2x2 + by2)dx + cxydy = 0 is made exact by multiplying the integrating factor 1/x2. Then the relation between and c is
If general solution of the differential equation ay'" + by" + cy’ + dy = 0 is linearly spanned by ex, sinx and cosx, then which one of the following holds?
If y = In (sin (x + a)) + b, where a and b are constants, is the primitive, then the corresponding lowest order differential equation is
What is the degree of the non-homogeneous partial differential equation,
Two linearly independent solutions of the differential equation y" - 2y' + y = 0 are y1 = ex and y2 = xex. Then a particular solution of y" - 2y' + y = ex sin x is
Consider the differential equation ( x + y + 1) dx + (2x + 2y + 1) dy = 0. Which of the following statements is true?
Which one of the following differential equations represents all circles with radius a?


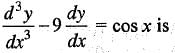
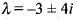


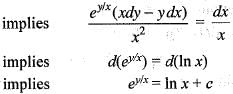
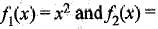 x |x| is zero for
x |x| is zero for
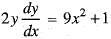
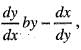 the equation of orthogonal trajectory is given by
the equation of orthogonal trajectory is given by
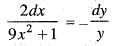
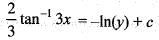
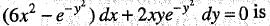
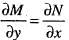 is satisfied, So, equation is exacct
is satisfied, So, equation is exacct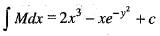 ...(i)
...(i)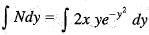 ...(ii)
...(ii)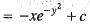
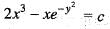
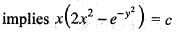
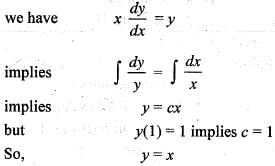
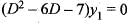
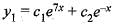
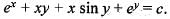
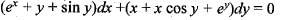
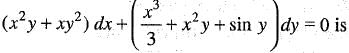
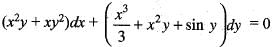
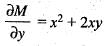

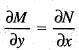
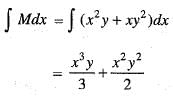
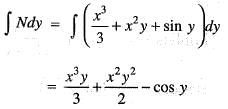

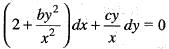
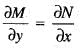
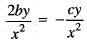

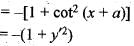
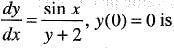
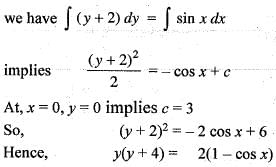
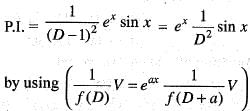
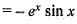
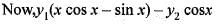
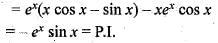
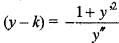 (iii)
(iii)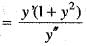 ...(iv)
...(iv)