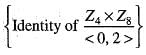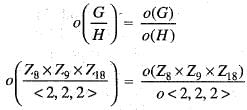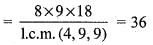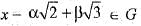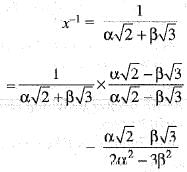Test: Group Theory - 9 - Mathematics MCQ
20 Questions MCQ Test - Test: Group Theory - 9
Assertion (A): A group can be isomorphic to its proper subgroup
Reason (R): The additive group Z of integer is isomorphic to (H, +) where
H = {mx : x ∈ Z and 0 ≠ m ∈ Z}
Reason (R): The additive group Z of integer is isomorphic to (H, +) where
H = {mx : x ∈ Z and 0 ≠ m ∈ Z}
The set of complex number z with | z | = 1 under the operation * denote by z1 * z2 = | z1 | ·z2
Let 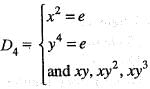
be the dihedral group of order 8. Then y-42 is equal to
In an infinite cyclic group G the number of automorphism is
If G1 and G2 are commulator subgroup and centre of the dihedral group D4 respectively. Then select the incorrect statement.
Let G be a group of order pq where p and q are prime numbers. Such that p > q then, G can have
If in a group a5 = e, aba-1 = b2 for a,b ε G, then o(b) is
Let D8 denote the group of symmetries of square (dihedral group). The minimal number of generators for D8 is
In the symmetric group Sn of degree n,n > 2 the set of all 3-cycles generates a subgroup of order
The number of non-empty even subsets (even set is the set having even number of elements) of a set having n elements is
Consider the alternating group A4 = {σ ε S4 : σ is an even permutation).
Which of the following is FALSE?
Let < (0,2) > denote the subgroup generated by (0,2) in Z4 x Z8. Then the order of (3, 1) + < (0, 2) > in the quotient group Z4 x Z8 / < (0,2) > is
The order o f the quotient group Z8 x Z9 x Z18/ < 2 , 2 , 2 > is
Let G be a group with respect to multiplication. If x = 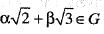 then x-1 is
then x-1 is
Let G be a group of order 8 generated by a and b such that a4 = b2 = 1 and ba = a3b. The order of the center of G is



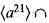
 are
are

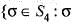 is an even permutation}
is an even permutation}