Test: Group Theory - 11 - Mathematics MCQ
20 Questions MCQ Test - Test: Group Theory - 11
Let σ = (125) (36) and t = (1456) (23) be two elements of the permutation group on 6 symbols. Then the product 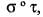 where
where 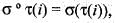 is
is
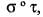 where
where 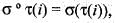 is
is The number of distinct group homomorphisms from (Z, +) onto (Z, +) is
A non empty set A is termed as an algebraic structure ________
Let S denote the group of all permutations on the finite set {1, 2, 3, 4, 5} under the operation of permutation multiplication. Then the order of the subgroup of S5 generated by  is
is
Let H be a subgroup Of ordet 60 of a group G of order 120. If a ε G/H, then which of the following is Not, a subgroup of G?
G is a group of order 51. Then which one of the following statements is false?
In the group {1, 2,........,16} under the operation of multiplication modulo 17, the order of the element 3 is
Let S be a non empty symmetric and transitive binary operation on a non empty set A. Consider any pair (a, b) ε S. Since S is symmetric, (b, a) ε S. Further, since S is transitive, (a, b) ε S. Which one of the following statements is true?
Let L be an equivalence relation on a set S of n elements, Consider the set Sa = {x : x ≠ a and aLx). Further, let D 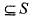 be such that no two elements in D are related under L. The number of elements in
be such that no two elements in D are related under L. The number of elements in 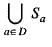 is at most
is at most
Let X denote the set of all real-valued functions defined on Z. Define a relation -in X by f ~ g if f(0)1 g(0). Then the relation ~ is
Let R be the ring o f p olynom ials over Z2 and let I be the ideal of R generated by the polynomial x2 + x + 1. Then the number of elements in the quotient ring R/ I is
If X Δ Z = Y Δ Z for the non-empty sets X, Y and Z, where Δ represents the symmetric difference then.
The number of elements of S5 (the symmetric group on 5 letters) which are their own inverses equals.
The number of group homomorphisms from the group ( Z18 ,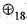 ) to the group ( Z30,
) to the group ( Z30,  )
)
Let G be a finite group and H be a normal subgroup G of order 2. Then the order of the center of G is





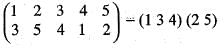
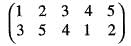 = L.C.M. ( 3 ,2 ) = 6
= L.C.M. ( 3 ,2 ) = 6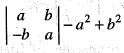
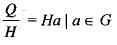 |
| is atmost
is atmost 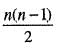 .
.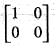 then A-1 does not exist.
then A-1 does not exist.

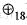 ) to group (Z30,
) to group (Z30, 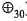 ) is equal to g.c.d.(18,30) = 6.
) is equal to g.c.d.(18,30) = 6.
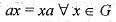

 = (1 2 10 12 7 6 3 8 11) (4 5 9)
= (1 2 10 12 7 6 3 8 11) (4 5 9)
















