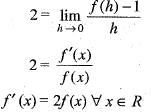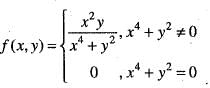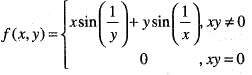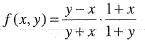Test: Functions Of One,Two Or Three Real Variables - 4 - IIT JAM MCQ
20 Questions MCQ Test - Test: Functions Of One,Two Or Three Real Variables - 4
Convert the set x in roster form if set x contains the positive prime number, which divides 72.
Let f(x + y) = f(x)f(y) for all x and y and f(5) = - 2 and f'(0) = 3. What is the value of f'(5)?
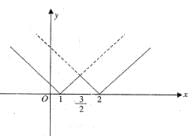
Let l = { 1 } ∪ { 2 } 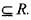 For x ∈ R, let φ(x) = dis (x, l) = ln f{| x —y | : y ∈ l} then
For x ∈ R, let φ(x) = dis (x, l) = ln f{| x —y | : y ∈ l} then
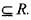 For x ∈ R, let φ(x) = dis (x, l) = ln f{| x —y | : y ∈ l} then
For x ∈ R, let φ(x) = dis (x, l) = ln f{| x —y | : y ∈ l} thenIf the function defined as
Then, the function f (x) has
Write the roaster form for A = {x : x2 – 5x + 6 = 0}
If we expand sinx by Taylor’s series about 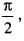 then a1, a7, a4, a3 are
then a1, a7, a4, a3 are
If f(x) is twice differentiable and | f(x) | < α, f'(x)| < β, in the range x > α, then which of the following is correct?
The function f(x) = | x + 2 | is not differentiable at a point
Using Rolle’s theorem, the equation. 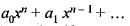
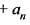 = 0 has atleast one root between 0 and 1, if
= 0 has atleast one root between 0 and 1, if
A function f : R-->R satisfies the e q .f(x +y) = f(x).f(y), 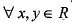 and f(x) ≠ 0,
and f(x) ≠ 0, 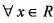 . If f(x) is differentiate at 0 a n d f'(0 ) = 2 then f'(x) is equal to
. If f(x) is differentiate at 0 a n d f'(0 ) = 2 then f'(x) is equal to
Which one of the following is true?


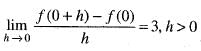
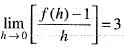
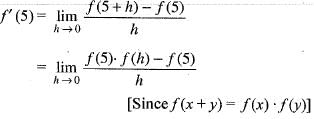
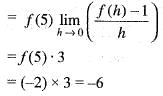 [by eq. (1)]
[by eq. (1)]
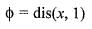
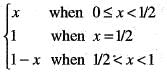
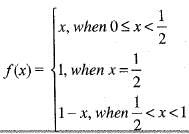
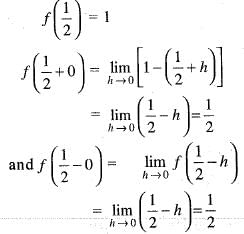

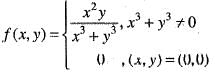
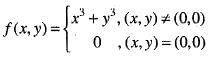

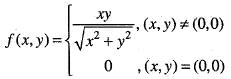
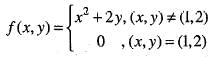
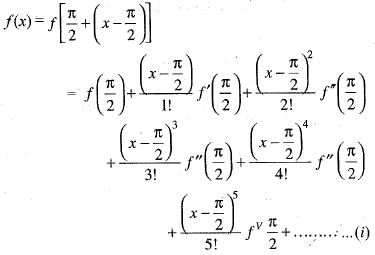
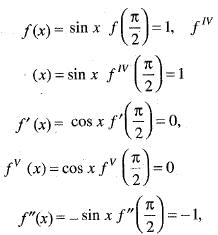
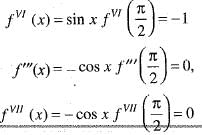
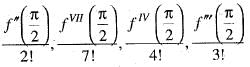
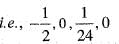
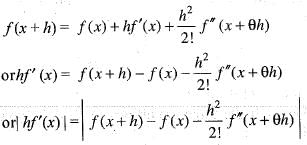

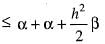
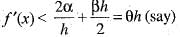
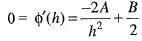
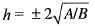
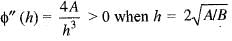
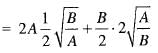
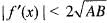
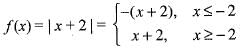
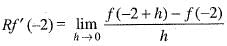

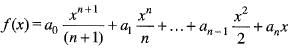 Since , f(x) is a polynomial, it is continuous and differentiable
Since , f(x) is a polynomial, it is continuous and differentiable x. Consequently f(x) is continuous in the closed interval [0, 1] and differentiable in the open interval [0,1] Also , f(0) = 0 and
x. Consequently f(x) is continuous in the closed interval [0, 1] and differentiable in the open interval [0,1] Also , f(0) = 0 and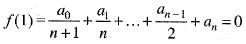
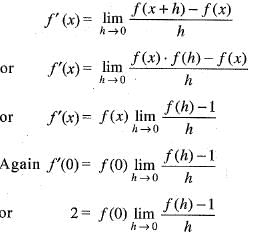
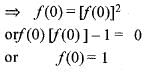
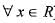 ]
]