Important Questions: Pair of Linear Equations in Two Variables - Year 10 MCQ

If two lines i.e. a pair of linear equations, has infinitely many solutions it means lines are overlapping each other i.e. coincident lines.

a₁ / a₂ = b₁ / b₂ = c₁ / c₂
2/4 = 3/6 = 5/10
1/2 = 1/2 = 1/2
So, a₁ / a₂ = b₁ / b₂ = c₁ / c₂ 
When these are equal then it is consistent.
Therefore option (C) is correct .

If am ≠ bl, then the equations ax+by=c, lx+my=n has a unique solution.

Given,

Pair of lines represented by the equations

ax + by = c

lx + my = n

For unique solution

For infinite solutions

For no solution

Given,

This can be transformed into

Therefore, If am ≠ bl, then the equations ax+by=c, lx+my=n has a unique solution.

The equation are y=0 and y=-7
y=0 is on the x-axis and y=-7 is the line parallel to the x-axes at a distance 7 units from y=0
The line will be parallel
if we try to solve these equations we get 0=7 which is absurd.
So the equations are inconsistent.
Therefore there is no solution.

Let the present age of father's be x years and present age of son's be y years.

According to the problem
x = 6y 
After 4 years
x + 4 = 4(y + 4)
Hence we get two equations
x = 6y ...(1)
x + 4 = 4(y + 4) ...(2)
Simplifying eq (2)
x + 4 = 4y + 16
x - 4y = 12
Put x = 6y in eq(2), we get
6y - 4y = 12
2y = 12
y = 6 years
and x = 6y = 36 years
Present age of son = 6 years
and present age of father = 36 years

By graphically in every condition, if a, b>>0; a, b< 0, a>0, b< 0; a<0, b>0 but a = b≠ 0.
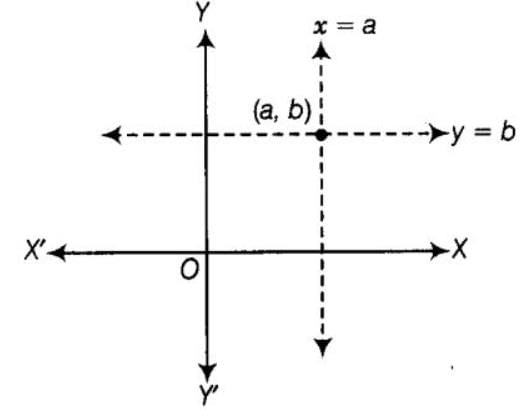
The pair of equations x = a and y = b graphically represents lines which are intersecting at (a, b).
If a, b > 0 

Similarly, in all cases two lines intersect at (a, b).

Lets,

First digit number = x

Second digit number = y

Number = (x+10y)

A/Q,

x + y = 9 ...................... (i)

A/Q,

(x+10y) = (10x+y) + 27

x + 10y = 10x + y +27

9x - 9y = 27

9(x - y) = 27

x - y = 27/9

x - y = 3 ......................... (ii)

Equation (i) and (ii) we get,

x = 3

Putting the value of x in eq.(i)

we get,

y = 6

Number = (10x +y)

= 10 x 3 + 6

= 30 + 6

= 36

x - 4y -14 = 0

x = 4y+14

putting this in 5x - y -13 = 0

5(4y+14) - y -13 =0

19y = -57     

y = -3

putting y = -3 in x = 4y+14

x = 4(-3)+14

x = 2

so option b is correct