Practice Test: Triangles - Grade 10 MCQ
10 Questions MCQ Test - Practice Test: Triangles
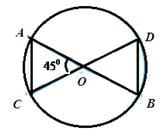
O is the point of intersection of two equal chords ABand CD such that OB = OD, then triangles OAC and ODB are

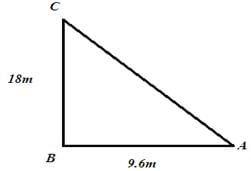
A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
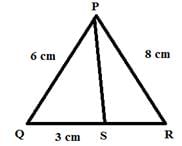
In triangle PQR, if PQ = 6 cm, PR = 8 cm, QS = 3 cm, and PS is the bisector of angle QPR, what is the length of SR?
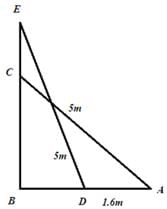
A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then the distance by which the top of the ladder would slide upwards on the wall is:
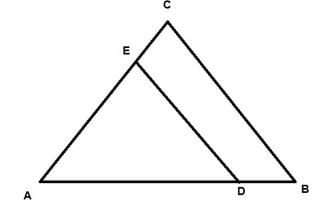
In the figure given below DE || BC. If AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, the value of x is:
If ΔABC ~ ΔDEF, AB = 4 cm, DE = 6 cm, EF = 9 cm and FD = 12 cm, find the perimeter of ABC.
The length of altitude of an equilateral triangle of side 8cm is
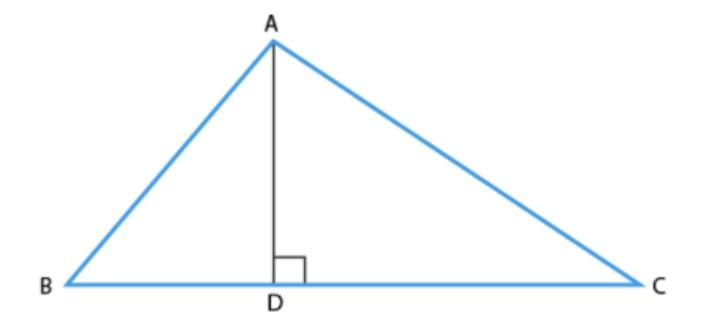
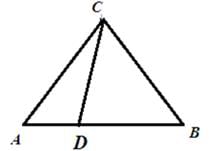
In the figure if ∠ACB = ∠CDA, AC = 8 cm and AD = 3 cm, find BD.
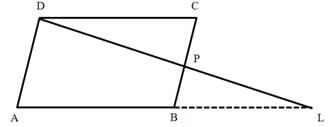
If ABCD is parallelogram, P is a point on side BC and DP when produced meets AB produced at L, then select the correct option