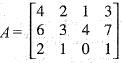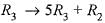Test: Linear Algebra - 5 - Mathematics MCQ
20 Questions MCQ Test - Test: Linear Algebra - 5
If 3x + 2 + z = 0
x + 4y + z = 0
2x + y + 4z = 0
be a system of equations, then
x + 4y + z = 0
2x + y + 4z = 0
be a system of equations, then
Let ω be a complex number such that ω3 = 1 but ω ≠ 1.
If A = 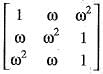 , then which of the following statementare true?
, then which of the following statementare true?
Let T : R2-->R 2 be a map defined by
T(x,y) = (x + y , x - y)
Which of the following statement is correct?
Consider the following linear transformation from the vector space R2 into the vector space R3.
T(x, y ) = (- x - y ,3x + 8y, 9x - 11y)
Then, the rank and nullity of T are respectively.
Define Ton R2 into itself by
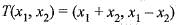
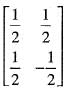
Then, matrix of T-1 relative to the standard basis for R2 is
Let T be linear transformation on R2 into itself such that T(1, 0) = (1, 2) and T(1, 1) = (0, 2). Then, T(a, b) is equal to
Let V be a vector space of 2 x 2 matrices over R. Let T be the linear mapping T : V —> V, such that
T(A) = AB - BA , where B = 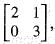 Then the nullity of T is
Then the nullity of T is
Let A be a 4 x 4 matrix with real entries such that - 1, 1, 2, - 2 are its eigen values. If B = A4 - 5A2 + 5I, where I denotes the 4 x 4 identity matrix, then which of the following statements are correct?
The characteristic polynomial of the 3 x 3 real matrix 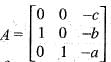 is
is
If the characteristic roots of 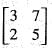 are λ1 and λ2 the characteristic roots
are λ1 and λ2 the characteristic roots 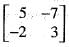 is
is
If A =  and I =
and I = 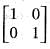 . Which of the following is the zero matrix?
. Which of the following is the zero matrix?
Let the characteristic equation of a matrix M be λ2 - λ - 1 = 0, then
If M is a 7 x 5 matrix of rank 3 and N is a 5 x 7 matrix of rank 5, then rank (MN) is
Consider the system of linear equations
x + y + z = 3 , x - y - z = 4, x - 5y + kz = 6
Then, the value of k for which this system has an infinite number of solutions is
For which value of A will the matrix given below become singular? 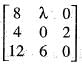


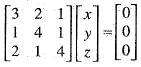
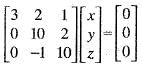
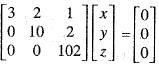
 . Then, the rank of M is equal to
. Then, the rank of M is equal to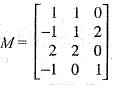
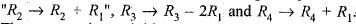 These operations yield.
These operations yield.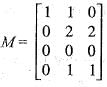
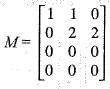

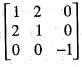 lie in the disc
lie in the disc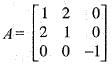
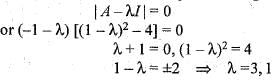
 is
is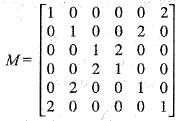
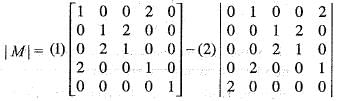
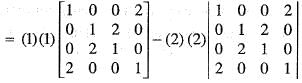
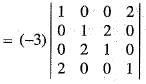
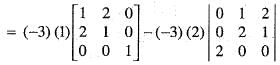
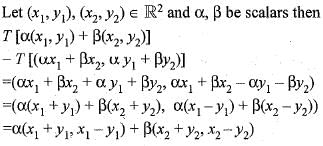
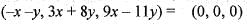 Comparing the components on both sides, we get
Comparing the components on both sides, we get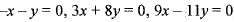 Solving for * and y, we get x = 0, y = 0.
Solving for * and y, we get x = 0, y = 0.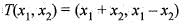
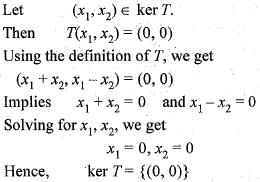 Implies T is one-one.
Implies T is one-one.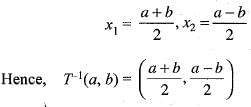
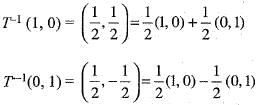
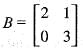
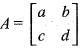 belongs to ker T
belongs to ker T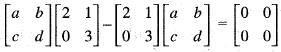
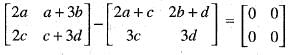 or equivalently,
or equivalently, 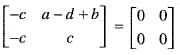
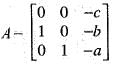
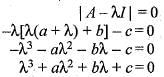

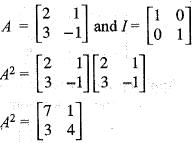
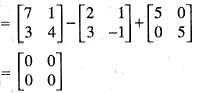
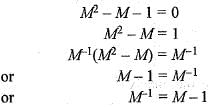
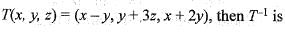

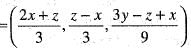
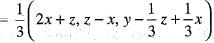

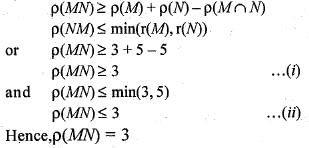
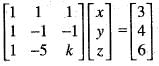

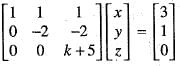
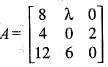
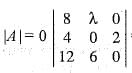 =0
=0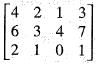 the rank of the matrix is
the rank of the matrix is