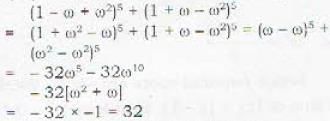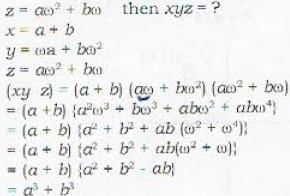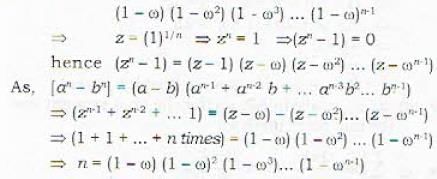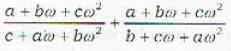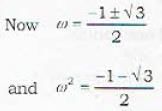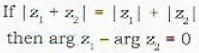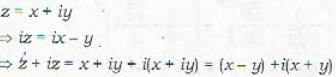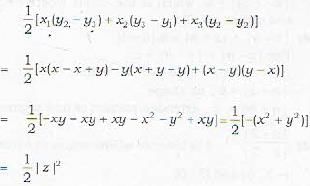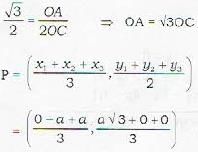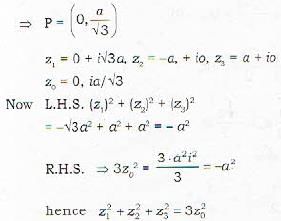Test:- Complex Number - 2 - Mathematics MCQ
20 Questions MCQ Test - Test:- Complex Number - 2
If z = x - iy and w = (1 - iz)/( z - l ) , then | w | = 1 implies that in the complex plane, z iies on
If the complex number z1, z2, z3 are in A.P. then they lies on a
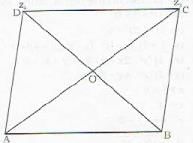
The point z1 , z2, z3, z4 in the complex plane are the vertices of a parallelogram taken in order if and only if.
If (1, ω, ω2)5 are the cube root of unity, then (1 - ω + ω2)5 + (1 + ω - ω2)5 =
If a, b are the complex cube roots of unity and x = a + b, y = ωa + bω2, z = aω2 - bω, then xyz =
If 1, ω, ω2 ... ωn-1 are the nth roots of unity then (1 - ω) (1 - ω2) ... (1 — ωn-2) is equal to
If ω, ω2 are the complex root of unity, then [(a + bω - cω2)/(c + aω + bω2)] + [(a + bω+ aω2)/ (b + cω + aω2)]
If cube root of unity are 1, ω, ω2, then the roots of the equation (x - 1)3 + 8 = 0 are
For any complex number z, the minimum value of |z| + | z - 1 | is
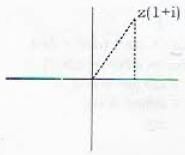
Multiplying a complex number z by 1 + i rotates the radius vector of z by an angle of
If |z1 + z2| = |z1| + |z2| , then arg z1 - arg z2 is equal to
The area of the triangle formed by the complex number z, iz, z + iz in the argand plane is
Let z be a complex number. Then the angle between z and iz is
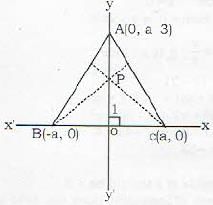
If z1, z2, z3 are vertices of equilateral triangle with zo as centroid, then z12 + z22 + z32 is equal to


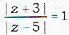 , it is bisector of line segment joining (-3.,0) and (5,0)
, it is bisector of line segment joining (-3.,0) and (5,0)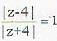 in the complex plane lies on
in the complex plane lies on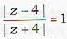

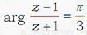 is
is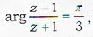 it is a circle
it is a circle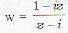
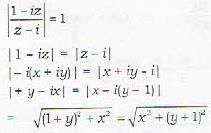
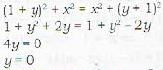
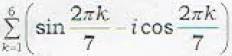 is
is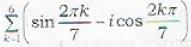 is
is