MCQ (Previous Year Questions) - Ellipse (Competition Level 1) - JEE MCQ
7 Questions MCQ Test - MCQ (Previous Year Questions) - Ellipse (Competition Level 1)
If distance between the foci of an ellipse is equal to its minor axis, then eccentricity of the ellipse is-
[AIEEE-2002]
The equation of an ellipse, whose major axis = 8 and eccentricity = 1/2, is
[AIEEE-2002]
The foci of the ellipse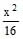 
+
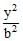= 1 and the hyperbola 
- 
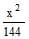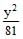= 1/25 coincide. Then the value of b2 is-
[AIEEE 2003]
+ = 1 and the hyperbola - = 1/25 coincide. Then the value of b2 is- The eccentricity of an ellipse, with its centre at the origin, is . If one of the directrices is x = 4, then the equation of the ellipse is-
[AIEEE 2004]
A focus of an ellipse is at the origin. The directrix is the line x = 4 and the eccentricity is 1/2. Then the length of the semi−major axis is
Statement1 : An equation of a common tangent to the parabola y2 = 16√3x and the ellipse 2x2 + y2 = 4 is y = 2x + 2√3
Statement 2: If the line 
is a common tangent to the parabola y2 = 16√3x and the ellipse 2x2 + y2 = 4, then m satisfies m4 + 2m2 = 24
[AIEEE 2012]
An ellipse is drawn by taking a diameter of the circle (x - 1)2 + y2 = 1, as its semi-minor axis and a diameter of the circle x2 + (y - 2)2 = 4 as its semi-major axis. If the centre of the ellipse is at the origin and its axes are the coordinate axes, then the equation of the ellipse is :
[AIEEE 2012]
Important Questions for MCQ (Previous Year Questions) - Ellipse (Competition Level 1)
MCQ (Previous Year Questions) - Ellipse (Competition Level 1)
Online Tests for MCQ (Previous Year Questions) - Ellipse (Competition Level 1)
|
© EduRev
|
Education Revolution
|
|
