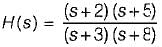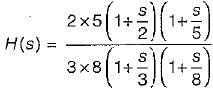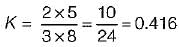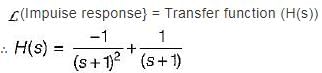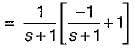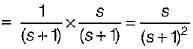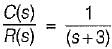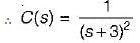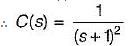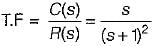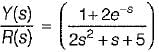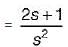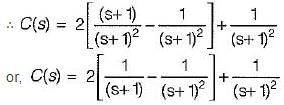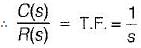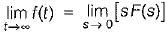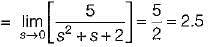Test: Transfer Function- 3 - Electronics and Communication Engineering (ECE) MCQ
15 Questions MCQ Test - Test: Transfer Function- 3
Match List - I (Roots in s-plane) with List - II (Corresponding impulse response) and select the correct answer using the codes given below the lists:
List - I
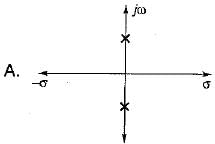
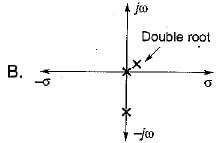
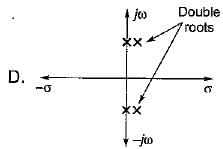
List - II

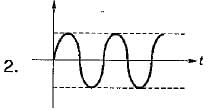
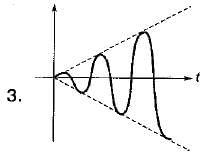
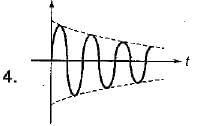
Codes:
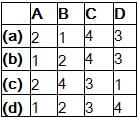
List - I




List - II




Codes:

The DC gain of the system represented by the following transfer function is
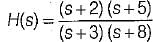
The unit impulse response of a control system is given by c(t) = -te-t + e-t. Its transfer function is
The impulse response of an initially relaxed linear system is e-3t u(t). To produce a response of te-3t u(t), the input must be equal to
A linear time invariant system, initially at rest when subjected to a unit step input gave response c(t) = te-t(t ≥ 0). The transfer function of the system is
A linear time invariant system having input r(t) and output y(t) is represented by the differential equation
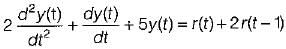
The transfer function of the given system is represented as
The open loop transfer function of a system is
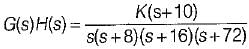
A closed loop pole will be located at s = -12
when the value of K is
The singularities of a function are the points in the s-plane at which the function or its derivates
Assertion (A): The final value theorem cannot be applied to a function given by
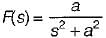
Reason (R): The function s F(s) has two poles on the imaginary axis of s-plane.
When two time constant elements are cascaded non-interactively then, the overall transfer function of such an arrangement
The unit impulse response of a unity feedback control svstem whose Open Iood transfer function
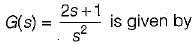
The impulse response of a linear time invariant system is a unit step function. The transfer function of this system would be
Consider the function 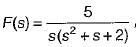 where F(s) is the Laplace transform of f(t)
where F(s) is the Laplace transform of f(t) 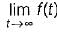 is equal to
is equal to