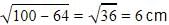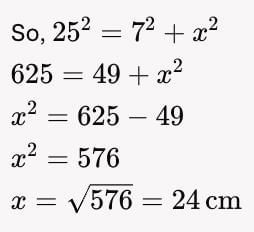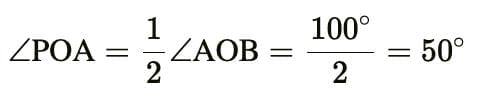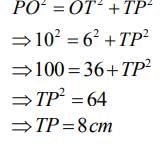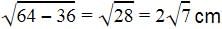Practice Test: Circles - Class 10 MCQ
15 Questions MCQ Test - Practice Test: Circles
A point P is 10 cm from the centre of a circle. The length of the tangent drawn from P to the circle is 8 cm. The radius of the circle is equal to
A point P is 25 cm from the centre of a circle. The radius of the circle is 7 cm and length of the tangent drawn from P to the circle is x cm. The value of x =
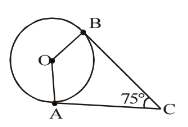
In fig, O is the centre of the circle, CA is tangent at A and CB is tangent at B drawn to the circle. If ∠ACB = 75°, then ∠AOB =
In fig, O is the centre of the circle. PQ is tangent to the circle and secant PAB passes through the centre O. If PQ = 5 cm and PA = 1 cm, then the radius of the circle is
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q such that OQ = 12 cm. Length PQ is
The length of the tangent from a point A at a circle, of radius 3 cm, is 4 cm. The distance of A from the centre of the circle is
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 80° then ∠POA is equal to
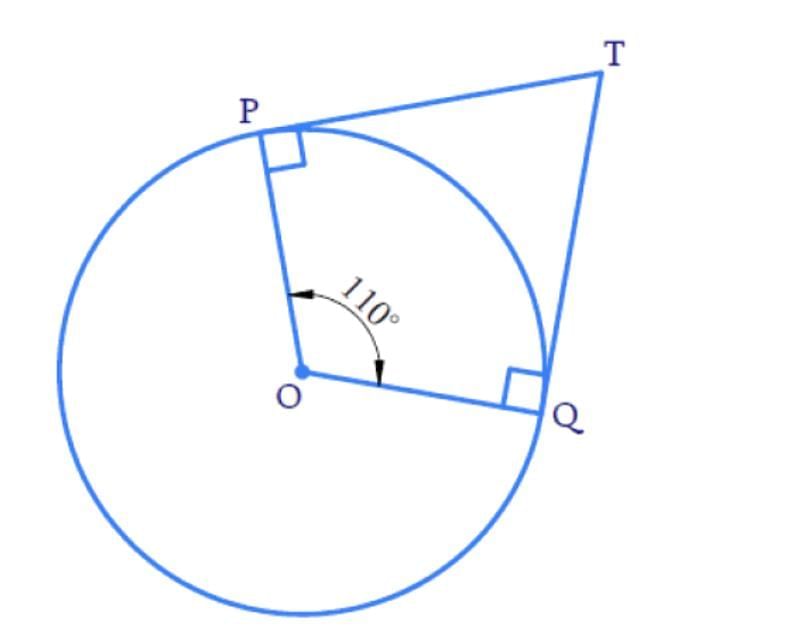
If TP and TQ are two tangents to a circle with centre O so that ∠POQ = 110°, then, ∠PTQ is equal to
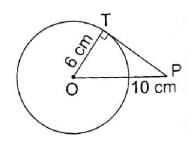
In the given figure, PT is tangent to the circle with centre O. If OT = 6 cm and OP = 10 cm then the length of tangent PT is
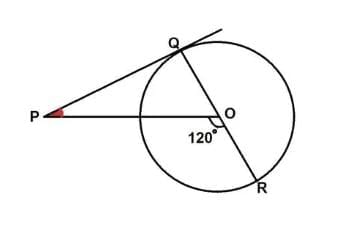
PQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that ∠POR = 120°, then ∠OPQ is
The length of the tangent drawn from a point 8 cm away from the centre of a circle of radius 6 cm is
If the diagonals of a cyclic quadrilateral are equal, then the quadrilateral is
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is a:
In the given figure, PQ is the tangent of the circle. Line segment PR intersects the circle at N and R. PQ = 15 cm, PR = 25 cm, find PN:
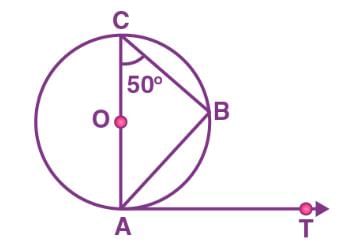
AB is a chord of the circle and AOC is its diameter such that angle ACB = 50°. If AT is the tangent to the circle at the point A, then BAT is equal to