Areas Related To Circles - Olympiad Level MCQ, Class 10 Mathematics - Class 10 MCQ
25 Questions MCQ Test - Areas Related To Circles - Olympiad Level MCQ, Class 10 Mathematics
Practice Test/Quiz or MCQ (Multiple Choice Questions) with Solutions of Chapter "Areas related to Circles" are available for CBSE Class 10 Mathematics (Maths) and have been compiled as per the syllabus of CBSE Class 10 Mathematics (Maths)
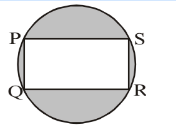
Q. In the adjoining figure PQRS is a rectangle 8 cm × 6 cm, inscribed in the circle. The area of the shaded
portion will be :
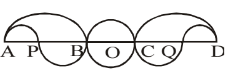
In the adjoining figure AB = CD = 2BC = 2BP = 2 CQ. In the middle, a circle with radius 1 cm is drawn. In the rest figure all are the semicircular arcs. What is the perimeter of the whole figure?
If BC passes through centre of the circle, then the area of the shaded region in the given figure is
Two circles of unit radii, are so drawn that the centre of each lies on the circumference of the other. The area of the region common to both the circles, is :
The area of the largest possible square inscribed in a circle of unit radius (in square unit) is :
The area of the largest triangle that can be inscribed in a semicircle of radius r is :
If a regular hexagon is inscribed in a circle of radius r, then its perimeter is :
If a regular hexagon circumscribes a circle of radius r, then its perimeter is :
In the adjoining figure there are three semicircles in which BC = 6 cm and BD = 6 3 cm. What is the area of the shaded region (in cm) :
ABCD is a square of side a cm. AB, BC, CD and AD all are the chords of circles with equal radii each. If the chords subtends an angle of 120° at their respective centres, find the total area of the given figure, where arcs are part of the circles :
In the adjoining figure PQRS is a square and MS = RN and A, P, Q and B lie on the same line. Find the ratio of the area of two circles to the area of the square. Given that AP = MS.
adjoining figure ABCD is a square. A circle ABCD is passing through all the four vertices of the square. There are two more circles on the sides AD and BC touching each other inside the square, AD and BC are the respective diameters of the two smaller circles. Area of the square is 16 cm2.
In the adjoining figure ABCD is a square. A circle ABCD is passing through all the four vertices of the square. There are two more circles on the sides AD and BC touching each other inside the square, AD and BC are the respective diameters of the two smaller circles. Area of the square is 16 cm2.
In the adjoining figure ABCD is a square. A circle ABCD is passing through all the four vertices of the square. There are two more circles on the sides AD and BC touching each other inside the square, AD and BC are the respective diameters of the two smaller circles. Area of the square is 16 cm2 What is the area of region 3?
A circular paper is folded along its diameter, then again it is folded to form a quadrant. Then it is cut as shown in the figure, after it the paper was reopened in the original circular shape. Find the ratio of the original paper to that of the remaining paper? (The shaded portion is cut off from the quadrant. The radius of quadrant OAB is 5 cm and radius of each semicircle is 1 cm) :
A square is inscribed in a circle then another circle is inscribed in the square. Another square is then inscribed in the circle. Finally a circle is inscribed in the innermost square. Thus there are 3 circles and 2 squares as shown in the fig. The radius of the outer-most circle is R.
What is the radius of the inner-most circle?
A square is inscribed in a circle then another circle is inscribed in the square. Another square is then inscribed in the circle. Finally a circle is inscribed in the innermost square. Thus there are 3 circles and 2 squares as shown in the fig. The radius of the outer-most circle is R. What is the sum of areas of all the squares shown in the figure?
A square is inscribed in a circle then another circle is inscribed in the square. Another square is then inscribed in the circle. Finally a circle is inscribed in the innermost square. Thus there are 3 circles and 2 squares as shown in the fig. The radius of the outer-most circle is R. What is the sum of areas of all the squares shown in the figure?
A regular hexagon is inscribed in a circle of radius R. Another circle is inscribed in the hexagon. Now another hexagon is inscribed in the second (smaller) circle. What is the sum of perimeters of both the hexagons?
A regular hexagon is inscribed in a circle of radius R. Another circle is inscribed in the hexagon. Now another hexagon is inscribed in the second (smaller) circle. What is the ratio of area of inner circle to the outer circle?
A regular hexagon is inscribed in a circle of radius R. Another circle is inscribed in the hexagon. Now another hexagon is inscribed in the second (smaller) circle. If there are some more circles and hexagons inscribed in the similar way as given above, then the ratio of each side of outermost hexagon (largest one) to that of the fourth (smaller one) hexagon is (fourth hexagon means the hexagon which is inside the third hexagon from the outerside.) :
In the adjoining diagram ABCD is a square with side 'a' cm. In the diagram the area of the larger circle with centre 'O' is equal to the sum of the areas of all the rest four circles with equal radii, whose centres are P, Q, R and S. What is the ratio between the side of square and radius of a smaller circle?
There are two concentric circles whose areas are in the ratio of 9 : 16 and the difference between their diameters is 4 cm. What is the area of the outer circle?
ABCD is a square, 4 equal circles are just touching each other whose centres are the vertices A, B, C, D of the square. What is the ratio of the shaded to the unshaded area within square?
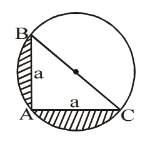
In the adjoining figure ACB is a quadrant with radius 'a'. A semicircle is drawn outside the quadrant taking AB as a diameter. Find the area of shaded region :




















