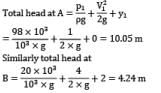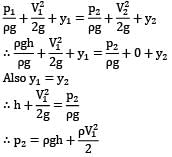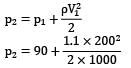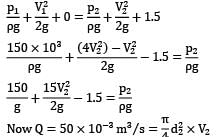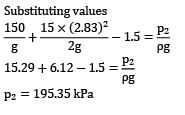All Courses
Get the App Signup / Login
Sign in Open App
Mechanical Engineering Exam  >  Mechanical Engineering Tests  >  Test: Fluid Dynamics Level - 1 - Mechanical Engineering MCQ

Test: Fluid Dynamics Level - 1 - Mechanical Engineering MCQ


Test Description

10 Questions MCQ Test - Test: Fluid Dynamics Level - 1

Test: Fluid Dynamics Level - 1 for Mechanical Engineering 2024 is part of Mechanical Engineering preparation. The Test: Fluid Dynamics Level - 1 questions and answers have been prepared according to the Mechanical Engineering exam syllabus.The Test: Fluid Dynamics Level - 1 MCQs are made for Mechanical Engineering 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Fluid Dynamics Level - 1 below.
Solutions of Test: Fluid Dynamics Level - 1 questions in English are available as part of our course for Mechanical Engineering & Test: Fluid Dynamics Level - 1 solutions in Hindi for Mechanical Engineering course. Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free. Attempt Test: Fluid Dynamics Level - 1 | 10 questions in 25 minutes | Mock test for Mechanical Engineering preparation | Free important questions MCQ to study for Mechanical Engineering Exam | Download free PDF with solutions
Test: Fluid Dynamics Level - 1 - Question 1
Save

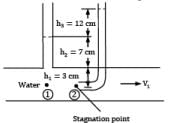
A piezometer and a Pitot tube are tapped into a horizontal water pipe, as shown in figure. The velocity of water at the center of the pipe is

Detailed Solution for Test: Fluid Dynamics Level - 1 - Question 1
Applying Bernoulli’s equation between point ① and ②

Considering basic assumptions of the equation to be applicable.

② is a stagnation point

i. e. V2 = 0 Also y1 = y2 Substituting the two conditions in Bernoulli’s equation

Test: Fluid Dynamics Level - 1 - Question 2
Save

Both free vortex and forced vortex can be expressed mathematically in terms of tangential velocity V at the corresponding radius r. Choose the correct combination.

Free vortex Forced vortex

Detailed Solution for Test: Fluid Dynamics Level - 1 - Question 2
A vortex represents motion of fluid mass revolving around an axis.

Free vortex is an example of irrotational flow represented by V × r = constant Forced vortex is an example of rotational flow given by V = r × constant

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: Fluid Dynamics Level - 1 - Question 3
Save

At point A in a pipeline carrying water, the diameter is 1 m, the pressure 98 kPa and the velocity 1m/s. At point B, 2 m higher than A, the diameter is 0.5 m and the pressure 20 kPa.

The direction of flow would be [

Detailed Solution for Test: Fluid Dynamics Level - 1 - Question 3
Applying continuity equation between sections at A and B

V2 = 4 m/s

Since Head at B is small. Flow occurs from A to B. The difference between two heads represents head loss.

Test: Fluid Dynamics Level - 1 - Question 4
Save

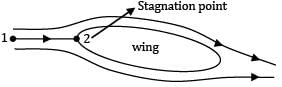
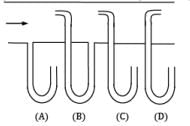
Which configuration measures the stagnation pressure?
Detailed Solution for Test: Fluid Dynamics Level - 1 - Question 4

Stagnation pressure head = p ρg + V2 / 2g

Configuration (A) will measure the gauge pressure in the pipe. Configuration (B) will measure the velocity head as the difference of height of manometric fluid. Configuration (C) will measure Gauge stagnation pressure. Configuration (D) is the same as (A).

Test: Fluid Dynamics Level - 1 - Question 5
Save

The pressure at a point in the fluid is 4.9 N/cm2. Find height when the fluid under consideration is in oil of specific gravity of 0.85.

Detailed Solution for Test: Fluid Dynamics Level - 1 - Question 5

Height = p / ρg 
= 48620 / 850 * 9.81 
= 5.83 m.

Test: Fluid Dynamics Level - 1 - Question 6
Save

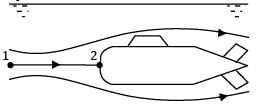
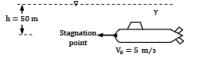
A submarine moves through seawater (SG = 1.03) at a depth of 50 m with velocity V0 = 5.0 m/s as shown in Fig. Determine the pressure at the stagnation point on the front of the submarine (in kPa).

Detailed Solution for Test: Fluid Dynamics Level - 1 - Question 6
Consider relative motion of water with respect to submarines.

Maybe the streamline formation will be as shown in the figure. Consider the center most straight streamline 1 → 2 where 1 is a point far away from the submarine where the fluid particle is actually at absolute rest but in another frame of reference i.e. with respect to the submarine it is moving with a speed of 5 m/sec. ∴ V1 = 5.0 m/sec.

V2 = 0

and as fluid is at absolute rest at 1, p1 = ρgh where h = 50 m Let us apply Bernoulli’s equation between 1 and 2.

p2 = 518090 Pa or 518.09 kPa

Note: Even though flow is unsteady in actual but by changing the frame of reference and writing motion relative to submarine flow becomes steady and Bernoulli’s equation is applicable.

Test: Fluid Dynamics Level - 1 - Question 7
Save

A light plane flies at 720 km/hr in standard air at an altitude of 1000 m. Determine the absolute stagnation pressure at the leading edge of the wing. Take, pair = 9.0 × 104 N/m2, ρ = 1.1 kg/m3.
Detailed Solution for Test: Fluid Dynamics Level - 1 - Question 7
Consider the cross-section of wing

Similar to previous question

Also, p1 = 9 × 104 Pa [for away point in atmosphere] V1 = 720 km/hr V1 = 200 m/sec y1 = y2

V2 = 0

Substituting these conditions in the Bernoulli’s equation

∴ p2 = 112 kPa

Test: Fluid Dynamics Level - 1 - Question 8
Save

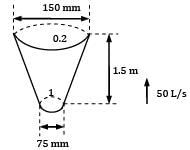
A vertical water pipe, 1.5 m long, diverges from 75 mm diameter at the bottom to 150 mm diameter at the top and the rate of flow is 50 L/s upwards. If the pressure at the bottom end is 150 kN/m2 , the pressure at the top will be nearly

(!) 195.2 kN⁄m2
Detailed Solution for Test: Fluid Dynamics Level - 1 - Question 8

p1 = 150 × 103

Q = 50 L/s

Applying continuity equation at 1 and 2

V1 x A1 = V2 x A2

V1/V2 = (150/75)2

V1=4 V2

Applying Bernoulli equation and 1 and 2

V2 = 2.83m/sec

Test: Fluid Dynamics Level - 1 - Question 9
Save

An open tank contains water upto a depth of 350 cm and above it an oil of specific gravity 0.65 for a depth of 2.5 m. Find the pressure intensity at the extreme bottom of the tank.

Detailed Solution for Test: Fluid Dynamics Level - 1 - Question 9

p = (specific gravity of water* height of water + specific gravity of oil* height of oil) * 9.81 
= 5.027 N/cm2.

Test: Fluid Dynamics Level - 1 - Question 10
Save

Statement (I): There exists a positive pressure difference between the inlet and throat of a venturi meter.

Statement (II): The coefficient of discharge of a venturi meter accounts for the nonuniformity of flow at both inlet and throat.
Detailed Solution for Test: Fluid Dynamics Level - 1 - Question 10
The throat section of a venturimeter has the highest velocity and hence by the application of Bernoulli’s equation, the lowest pressure. So there is a positive pressure difference between the inlet and throat of a venturimeter, even if the flow is ideal, uniform and has no losses. The coefficient of discharge in the venturimeter is to compensate for the error due to non-uniformity of flow, as well as losses in the flow. Hence both statements are correct but (II) is not the collected explanation for statement (I).

Information about Test: Fluid Dynamics Level - 1 Page
In this test you can find the Exam questions for Test: Fluid Dynamics Level - 1 solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Fluid Dynamics Level - 1, EduRev gives you an ample number of Online tests for practice

Top Courses for Mechanical Engineering

Download as PDF

Top Courses for Mechanical Engineering

Important Questions for Fluid Dynamics Level - 1

Find all the important questions for Fluid Dynamics Level - 1 at EduRev.Get fully prepared for Fluid Dynamics Level - 1 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Fluid Dynamics Level - 1 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Fluid Dynamics Level - 1 resources.

Fluid Dynamics Level - 1 MCQs with Answers

Prepare for the Fluid Dynamics Level - 1 within the Mechanical Engineering exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Fluid Dynamics Level - 1

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Fluid Dynamics Level - 1 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup