Test: Fluid Kinematics Level - 2 - Mechanical Engineering MCQ
15 Questions MCQ Test - Test: Fluid Kinematics Level - 2
A 2-D flow defined by velocity field ⃗V⃗ = (x + 2y + 2)î + (4 − y)ĵ is
A stream function is given by (x2 − y2). The velocity potential function of the flow will be
The velocity potential function of a flow field is given by x2 − y2 + constant. Its stream function will be given by
The area of a 2 m long tapered duct decreases as ! = (0.5 − 0.2x) where ‘x’ is the distance in meters. At a given instant a discharge of 0.5 m3⁄s is flowing in the duct and is found to increase at a rate of 0.2 m3 /s2. The local acceleration (in m⁄s2) at x = 0 will be
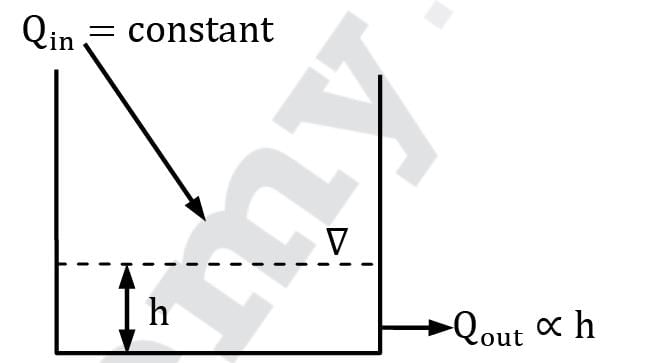
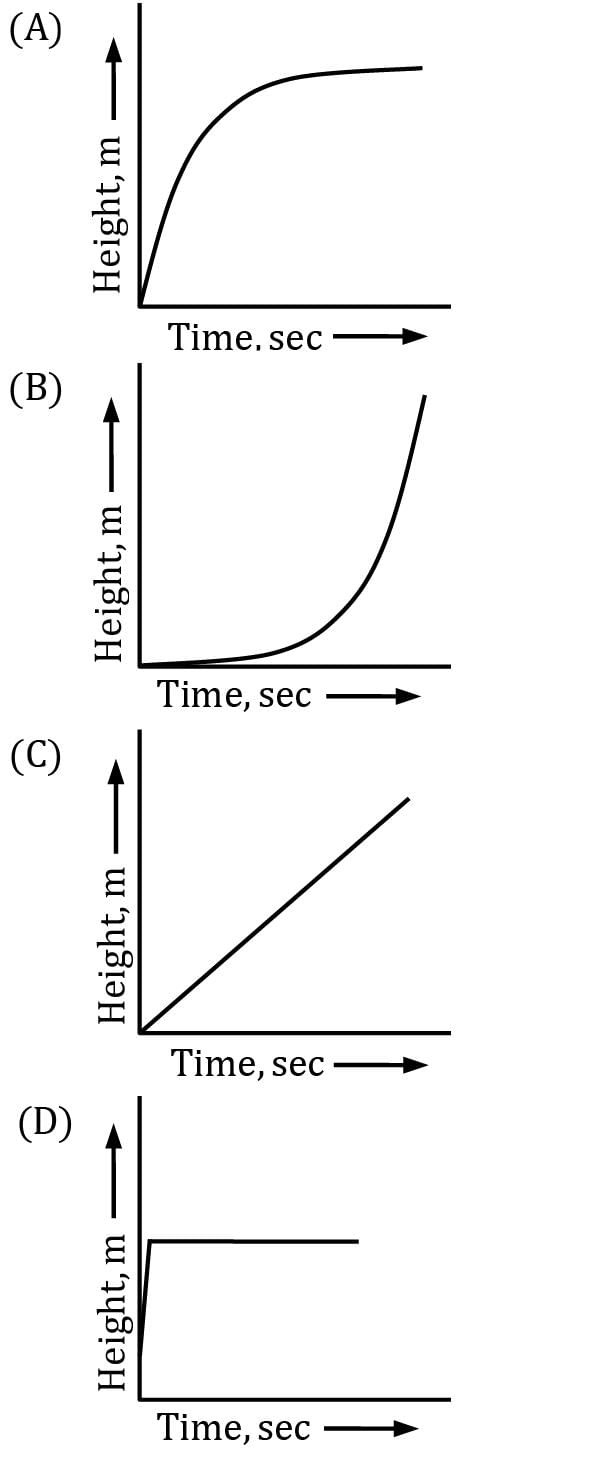
Water flows into an open drum from the top at a constant mass flow rate. Water exits through a pipe near the base with a mass flow rate proportional to the height of the liquid. If the drum is initially empty, which of the following gives the plot of liquid height with time?
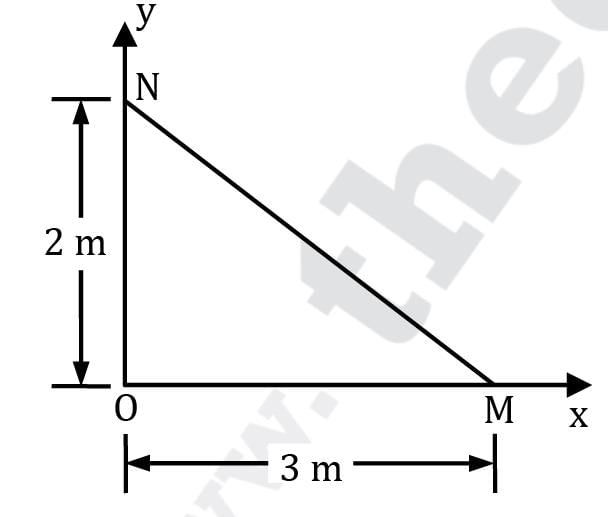
A stream function is given by ψ = 4x2y + (2 + t) y2 Find the flow rates across the faces of the triangular prism OMN (Fig.) having a thickness of 5 m in the z-direction at the time instant t = 2 seconds. (in m3/s)
For a two-dimensional potential flow, the velocity potential function is given by ϕ = 4x(3y − 4). The numerical value of stream function at the point (2, 3) is
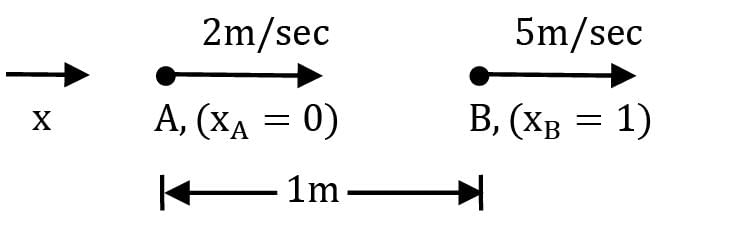
In a stream line steady state flow, two points A and B on a stream line are 1 m apart and the velocity of a particle varies linearly from 2 m/s to 5 m/s as the particle moves from A to B. What is the acceleration of fluid at B?
Statement I: When flow is unsteady, both normal and tangential components of acceleration will occur.
Statement II: During unsteady flow, in addition to the change of velocity along the path, the velocity will also change with time.
Statement I: Non-viscous flow between two plates held parallel with a very small spacing between them is an example of irrotational flow.
Statement II: Forced vortex implies irrotational flow.
The stream function for a flow field is ψ = 3x2 y + (2 + t)y2. The velocity at a point P for position vector r = î + 2ĵ − 3k̂ at time t = 2 will be
In a two-dimensional incompressible steady flow, the velocity component u = !ex is obtained. What is the other component v of velocity?
The instantaneous velocity and density fields for flow through a diffuser are given as u = u0 e−2x/L and ρ = ρ0 e−x/L Find the rate of change of density for the same time instant at x = L.
State whether the following flow field is physically possible? u = 3xy2 + 2x + y2 and v = x2 − 2y − y3
Which of the following statements is correct in respect of velocity potential function & stream function?
1. Stream function is defined only for an incompressible irrotational flow
2. Velocity Potential function is defined only for an incompressible irrotational flow
3. If the stream function exists it shall definitely satisfies the Laplace equation
4. If the velocity potential function exists it shall definitely satisfies the Laplace equation