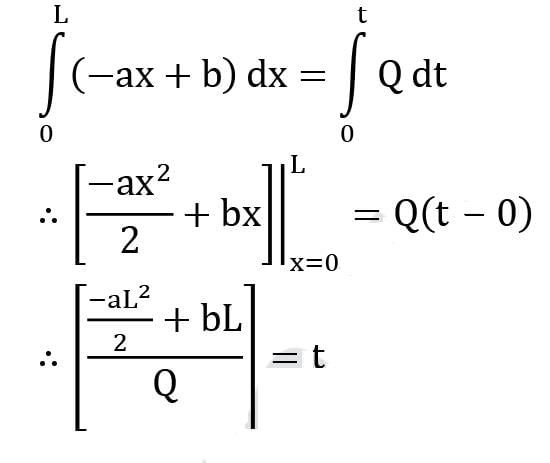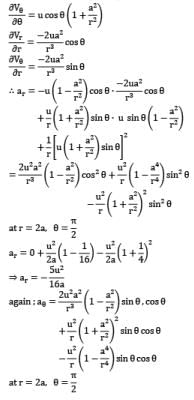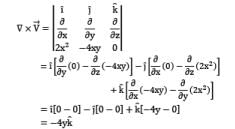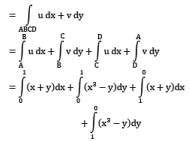Test: Fluid Kinematics Level - 3 - Mechanical Engineering MCQ
15 Questions MCQ Test - Test: Fluid Kinematics Level - 3
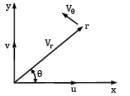
In cylindrical coordinates, a flow field is described as Vr = cos θ /r 2
Vθ = sin θ / r 2
Find the equation of streamline passing through the point (r = 2, θ = π/2).
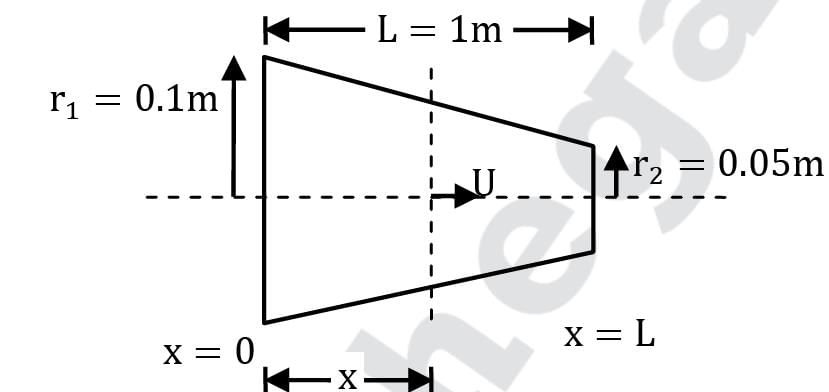
Consider steady state flow of an incompressible fluid (density ρ) through a conical diffuser of length L whose diameter varies from d1 at inlet to d2 at outlet. (d1 < d2 ). Find the acceleration in the flow at x = L.
In a steady state flow, the velocity components are u = 2kx ; v = 2ky ; w = −4kz Find the equation of streamline passing through the point (1, 0, 1).
A conical flow passage converges uniformly from 0.2 m diameter to 0.1 m diameter over a length of 1 metre. Find the magnitude of total acceleration at the middle of the diffuser.
Consider the following case.
Rate of flow varies linearly from 100 litres/s to 200 litres/s in 5 seconds and the time of interest is t = 2 sec.
(Velocity at any cross-section may be assumed to be uniform and perpendicular to the center line of passage).
Velocity distribution at entry to the pump intake is inversely proportional to square of radial distance from inlet to suction pipe. If the velocity at a radial distance of 1 m from the pipe inlet is 0.75 m/s, make calculations for the acceleration of flow at 0.5 m and 1.5 m from the inlet. Consider the streamlines to be radial.
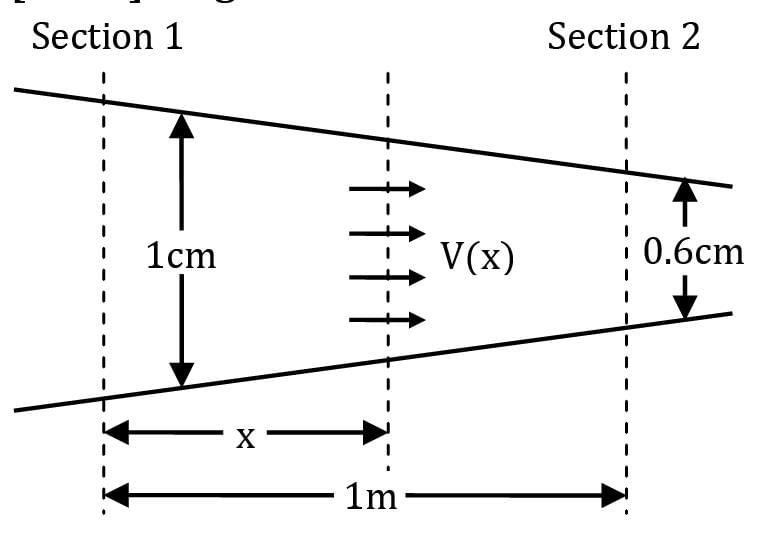
From a flow net diagram it is observed that distances between two consecutive streamlines at two consecutive cross-sections are 1 cm and 0.6 cm respectively. If the two sections are 1 m apart and velocity at the first section is 1 m/sec, find out the time taken by a fluid particle to move from the first to second section.
For a flow passage described by A(x) = −ax + b [Where A is the cross-sectional area at a distance x from inlet and a, b are constants] predict the time taken by a fluid particle to move from inlet to outlet of the flow. The length of the flow passage is L. The flow through the passage is steady and free of compressibility and viscous effects.
Also it can be assumed that flow velocity at a section is uniform and parallel to the centerline of the passage. The flow rate through the passage is Q.
A two-dimensional flow in cylindrical polar coordinates is given by Vr = 2r sin θ cos θ Vθ = −2r sin2 θ Check whether these velocity components represent a physical possible flow field.
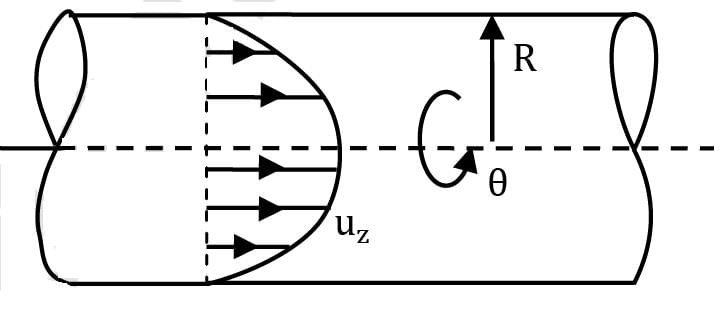
Consider fully developed axisymmetric Poiseuille flow in a round pipe of radius R with a pressure gradient (∂p/ ∂x) driving the flow as shown in figure (∂p/ ∂x is uniform and negative). The flow is steady, incompressible and axisymmetric about the x-axis. The velocity components are given by
uz = 1 / 4μ ( ∂p / ∂x ) (r2 − R2 ); ur = 0; uθ = 0
Find the acceleration of a fluid particle at the point r = 2a, θ = π/2 for a 2-D flow given by
Vr = −u (1 −a2 / r2) cos θ
Vθ = u (1 + a2 / r2 ) sin θ
A spherical balloon is filled with 3536π cubic meters of helium gas. If a leak in the balloon causes the gas to escape at the rate of 70π cubic meters per minute, then the rate (in meters per minute) at which the radius of the balloon decreases 50 minutes after the leakage began is
A flow field is defined by the stream function ψ = 2x2 y, determining the corresponding velocity potential.
Obtain the relationship between stream function ψ and the velocity components Vr and Vθ in cylindrical polar coordinates.
A two-dimensional flow field is prescribed by the velocity components: u = ky and v = 0 where k is an arbitrary constant. Find the circulation about a closed contour conforming to the equation x2 + y2 − 2ay = 0.
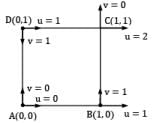
If the velocity field is given by: u = x+y and v = x3 −y Find the circulation around a closed contour defined by x = 1 ; y = 0, y = 1 and x = 0.