Test: Pressure & Fluid Statics Level - 2 - Civil Engineering (CE) MCQ
20 Questions MCQ Test - Test: Pressure & Fluid Statics Level - 2
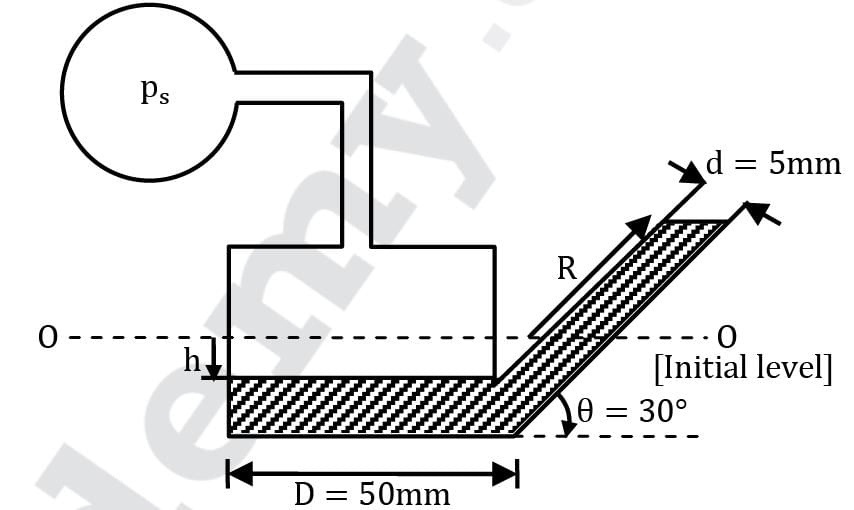
An inclined tube manometer measures the gauge pressure ps of a system S (Fig.). The reservoir and tube diameters of the manometer are 50 mm and 5 mm respectively. The inclination angle of the tube is 30°. What will be the percentage error in measuring Ps if the reservoir deflection is neglected?

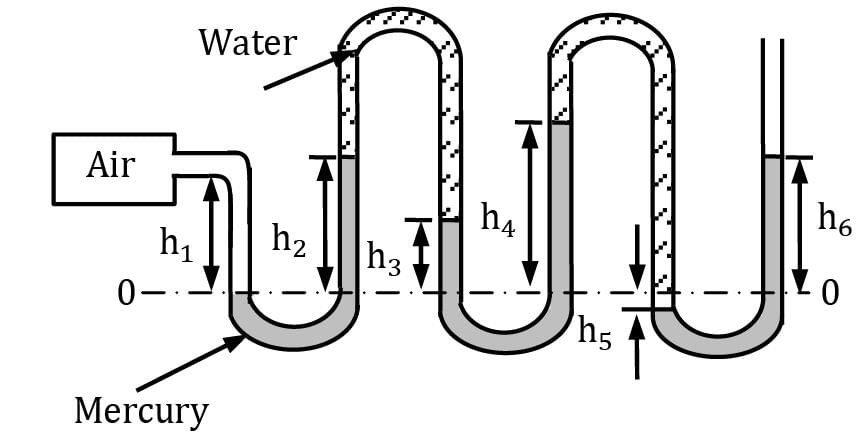
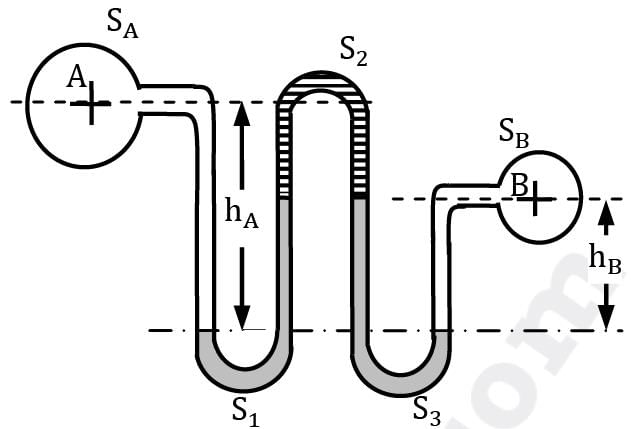
A multi-tube manometer using water and mercury is used to measure the pressure of air in a vessel, as shown in the Fig. For the given values of heights, calculate the gauge pressure (in kPa) in the vessel.
h1 = 0.4 m, h2 = 0.5 m,
h3 = 0.3 m, h4 = 0.7 m,
h5 = 0.1 m and h6 = 0.5 m.

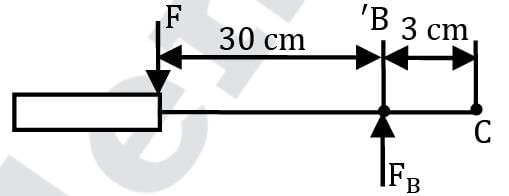
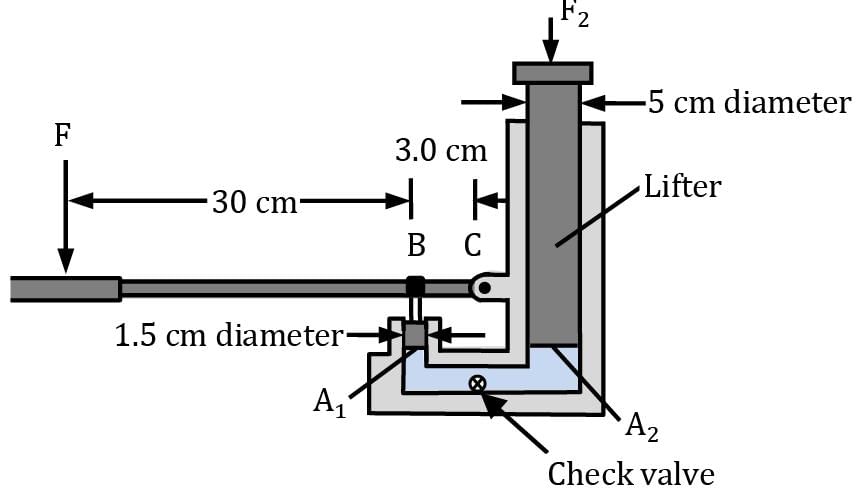
A hydraulic jack has the dimensions as shown. If one exerts a force F of 100 N on the handle of the jack, what load F2 (in kN) can the jack support? Neglect lifter weight.

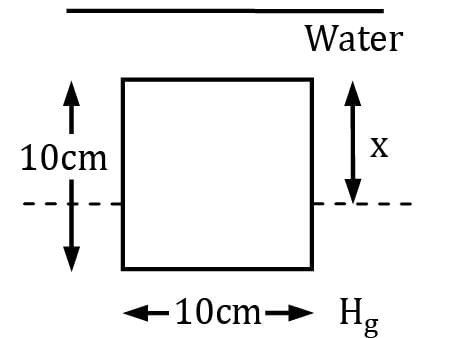
A metallic cube of side 10 cm, density 6.8 gm/cc is floating in liquid mercury (density 13.6 gm/cc), with 5 cm height of the cube exposed above the mercury level. Water density 1 gm/cc) is filled over this, to submerge the cube fully. The new height of cube exposed above mercury level is
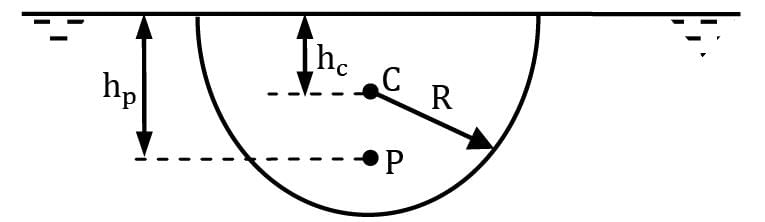
Consider a semi-circular surface of a submerged body as shown.

The top surface of water coincides with the diameter of the semi-circle. Find out the depth of the center of pressure for the surface.
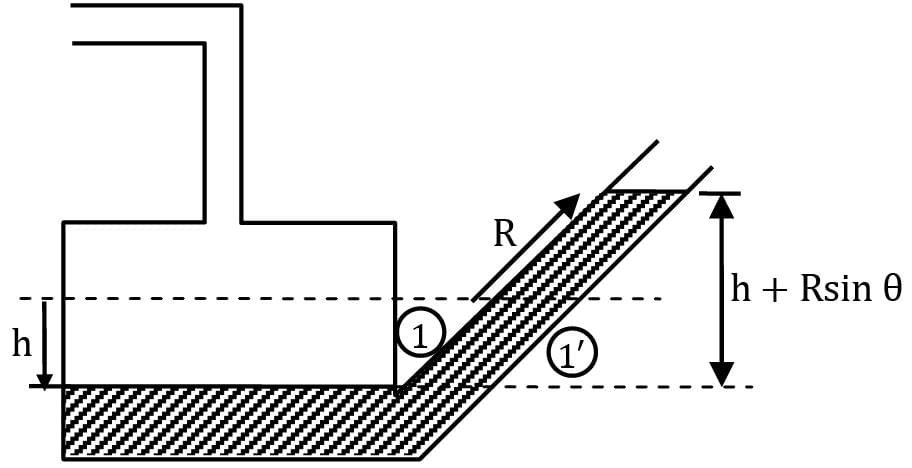
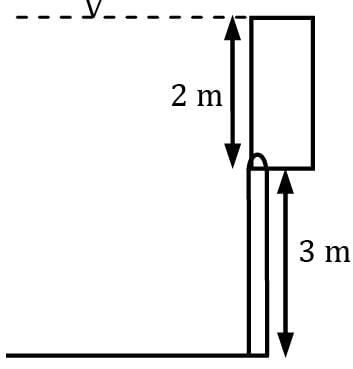
A cylindrical container whose weight is 79 N is inverted and pressed into the water, as shown in Figure. Determine the force F needed to hold the container at the position shown.
A double U-tube manometer is connected to two liquid lines A and B. Relevant heights and specific gravities of the fluids are shown in the given figure. The pressure difference, in head of water, between fluids at A and B is
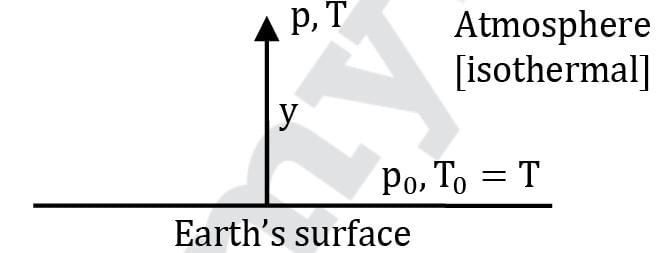
Which of the following options represents the variation of pressure with altitude in an isothermal atmosphere? The symbols have the usual meanings.
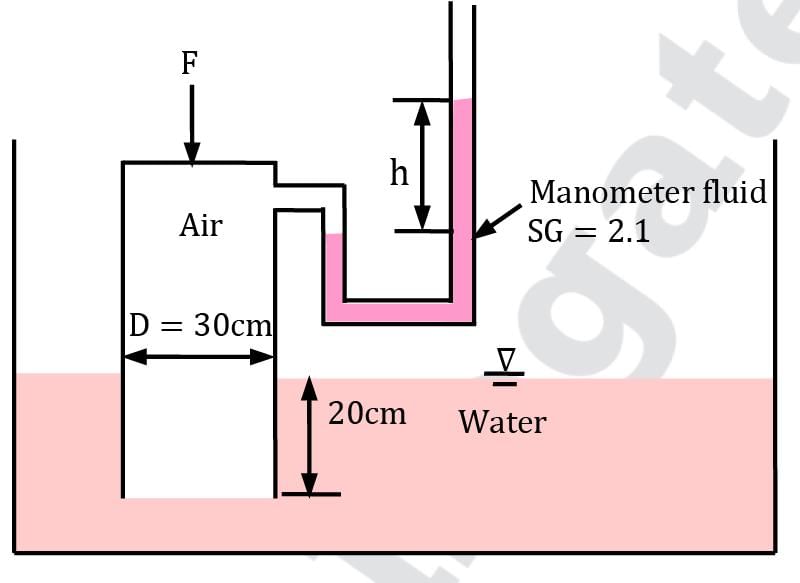
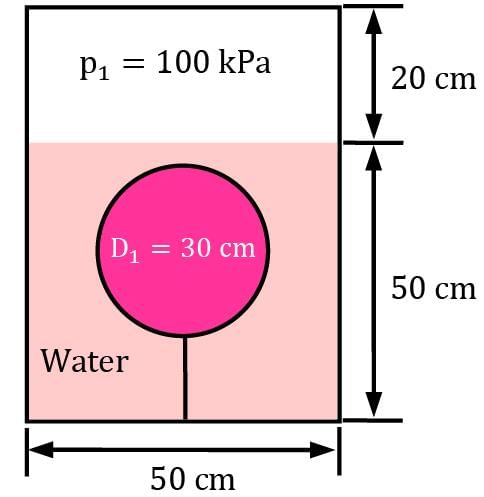
An elastic air balloon having a diameter of 30 cm is attached to the base of a container partially filled with water at +4°C, as shown in Figure. If the pressure of air above water is gradually increased from 100 kPa to 1.6 MPa, will the force on the cable change? If so, what is the percent change in the force? Assume the pressure on the free surface and the diameter of the balloon are related by p = CDn , where C is a constant and n = −2. The weight of the balloon and the air in it is negligible.
The specific weight W of ocean water changes according to the equation W = WO + C√h with depth h from the top surface. WO = Specific weight of ocean water at free surface and C is a constant. The pressure as a function of depth h is given by
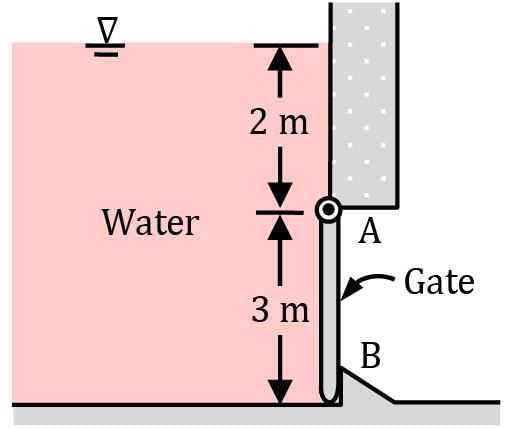
A 3-m-high, 6-m-wide rectangular gate is hinged at the top edge at A and is restrained by a fixed ridge at B. Determine the hydrostatic force exerted on the gate by the 5-m-high water and the location of the pressure center.
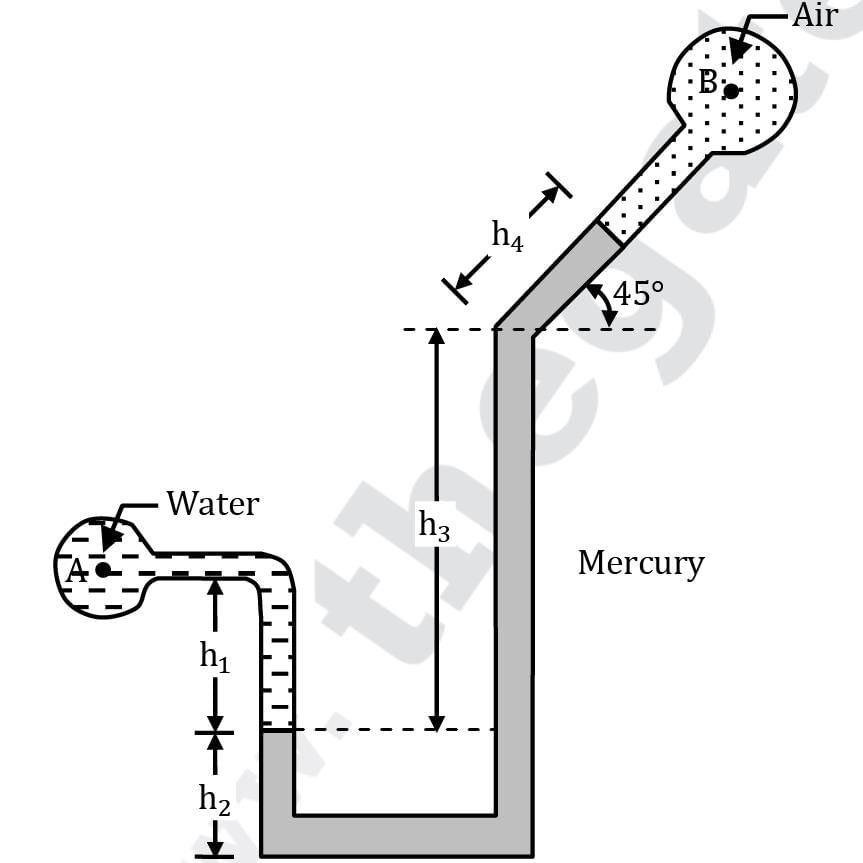
For the set-up shown in Fig. make calculations for the pressure difference between tanks A and B. Neglect the air column in the inclined tube and take h1 = 30 cm, h2 = 15 cm, h3 = 45 cm and h4 = 20 cm.
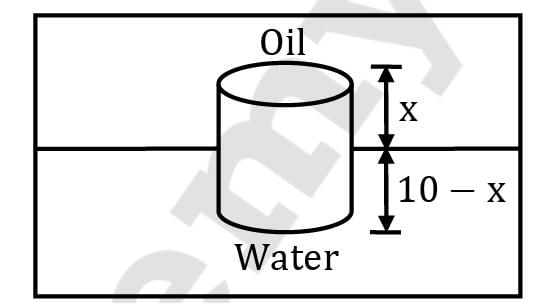
A big container filled with water and oil (S = 0.6) is shown in the figure.
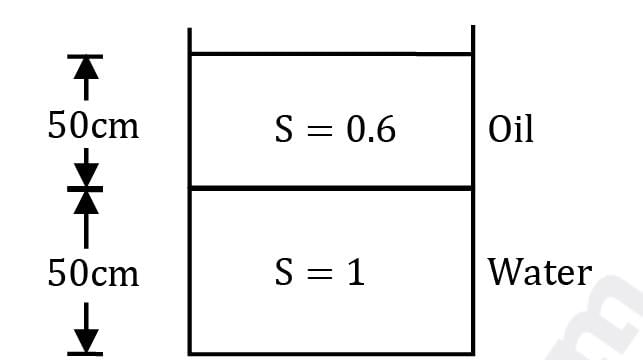
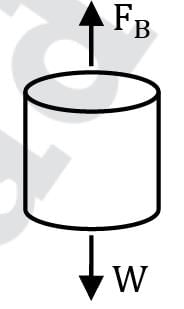
A vertical cylinder of density 900 kg/m3 and height 10 cm is dropped in the container. Which of the following options is correct?
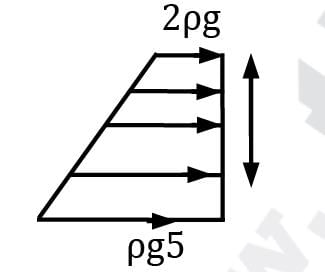
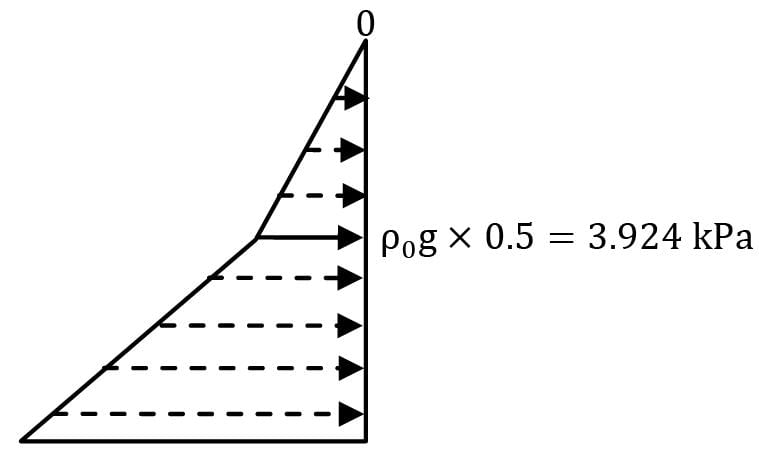
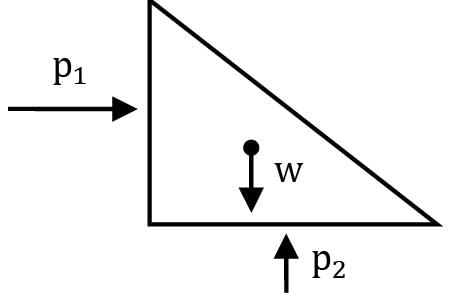
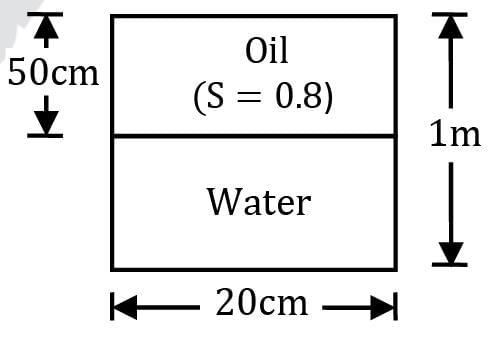
Consider a container filled with oil and liquid as shown in the below figure. What is the net pressure force (in kN) that acts on the side surface of container per unit width of container. (Perpendicular to the plane of paper).
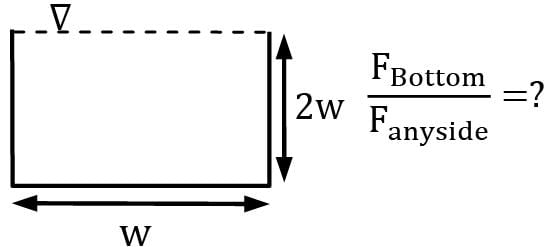
A house-top water tank is made of flat plates and is full to the brim. Its height is twice that of any side. The ratio of total thrust force on the bottom of the tank to that on any side will be
Consider the following statements:
The increase in metacentric height
1. Increases stability
2. Decreases stability
3. Increases comfort for passengers in a ship
4. Decreases comfort for passengers in a ship
Which of the above statements are correct?
A pipe line which is 4 m in diameter contains a gate valve. The pressure at the center of the gate (when closed) is 1.962 bar. Find the distance (in centimeter) of the center of pressure from centroid in meters for the gate. The oil in the pipeline has specific gravity of 0.87.
The density in a liquid varies as ρ(h) = 400 + 10h kg/m3 where ρ is the density at a point h meters below the free surface. Find out pressure at a point 8 m below the free surface.
Which of the following statements regarding manometers is incorrect?
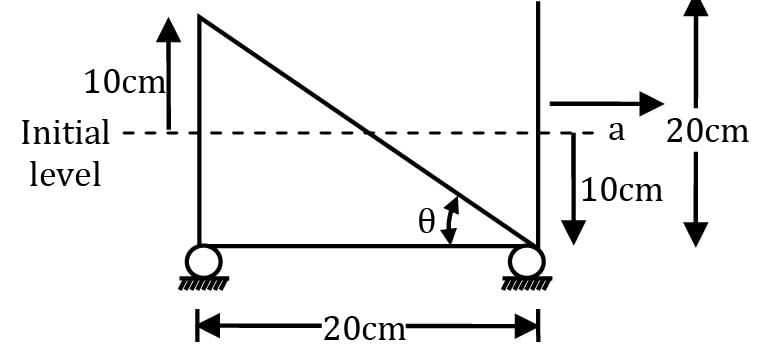
Consider a tank of length 20 cm and unit width perpendicular to a plane of paper filled with water upto a height of 10 cm. The tank starts moving with a constant acceleration along a horizontal direction such that the level of water in the front goes down by 10 cm. What is the force acting on the rear end of the container?