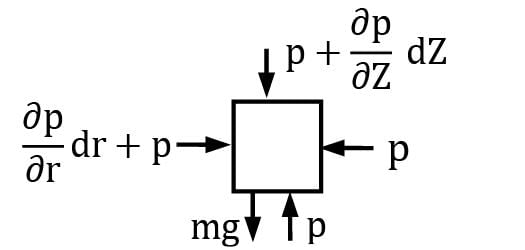
Test: Pressure & Fluid Statics Level - 3 - Mechanical Engineering MCQ
20 Questions MCQ Test - Test: Pressure & Fluid Statics Level - 3
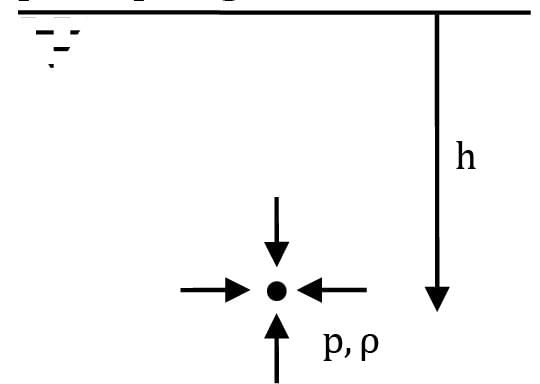
What is the intensity of pressure (in MPa) in the ocean at a depth of 1500 m. The salt water is compressible and weighs 10050 N/m3 at the free surface? E (bulk modulus of elasticity of salt water) = 2070 MN/m2 (constant).
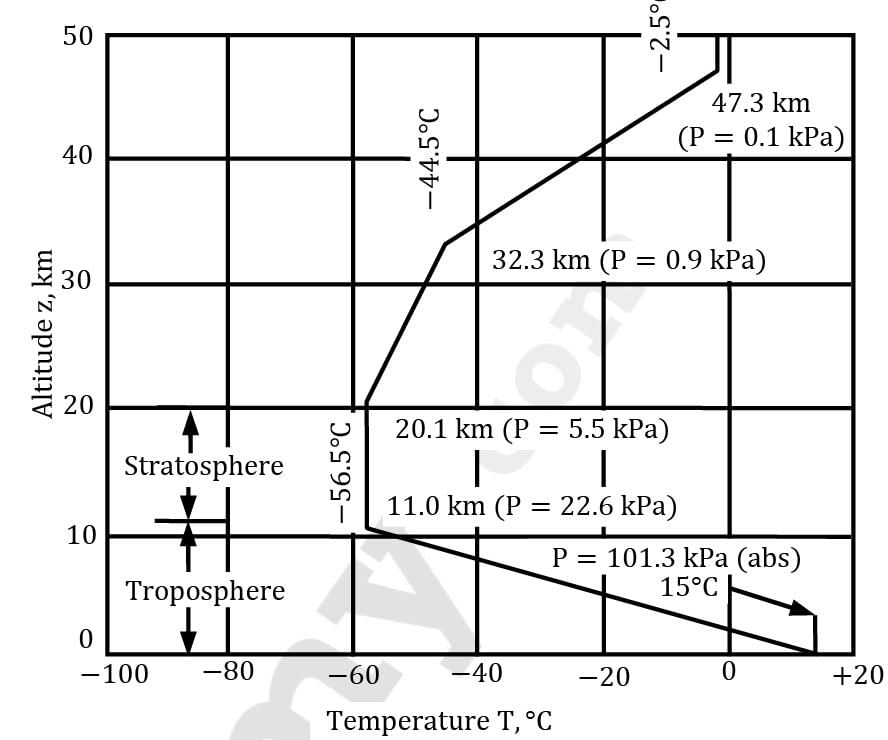
Treating the atmospheric air to be an ideal gas, what shall be the atmospheric pressure (in kPa) at the top of the skyscraper Bhurj Khalifa in Dubai standing tallest since 2008 with a height of 828 m. Consider the given variation of atmospheric condition with altitude. The characteristic gas constant for atmospheric air can be considered as 287 J / kg-K

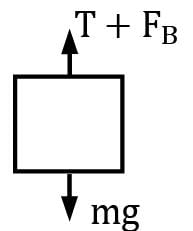
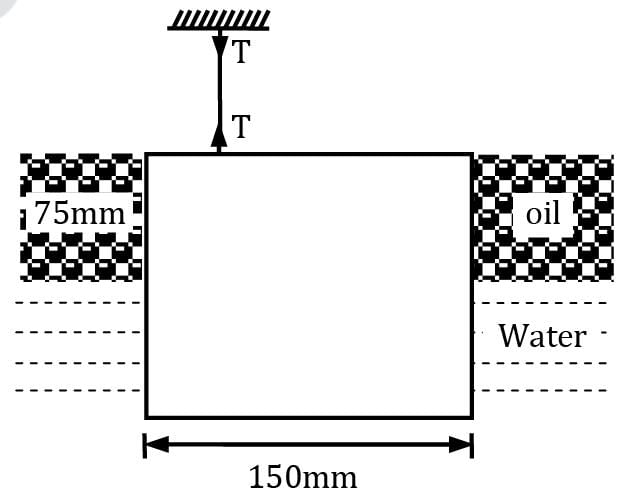
An aluminium cube 150 mm on a side is suspended by a string in oil and water as shown in figure. The cube is submerged with half of it being in oil and the other half in water. Find the tension in the string if the specific gravity of oil is 0.8 and the specific weight of aluminium is 25.93 kN/m3 .

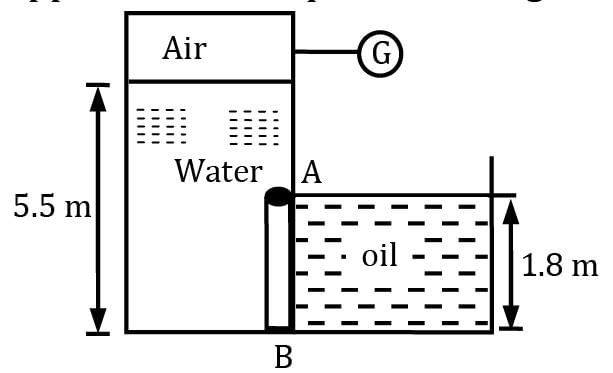
Gate AB in figure is 1.2 m wide (in a direction perpendicular to the plane of the figure) and is hinged at A. Gauge G reads −0.147 bar and oil in the right hand tank is having a relative density 0.75. What horizontal force must be applied at B for equilibrium of gate AB?
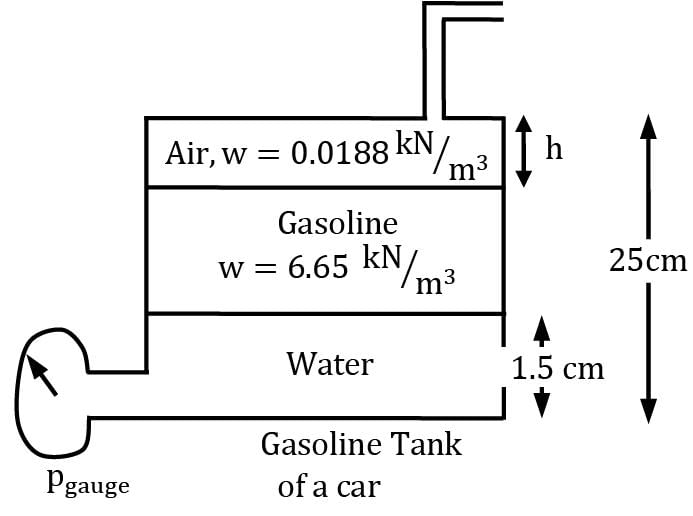
Consider the gasoline tank of a Maruti Suzuki Swift. Somehow water enters the fuel tank as shown. If for the given configuration, the reading on the fuel meter is full, Find out height of air column (h in cm) in the tank.
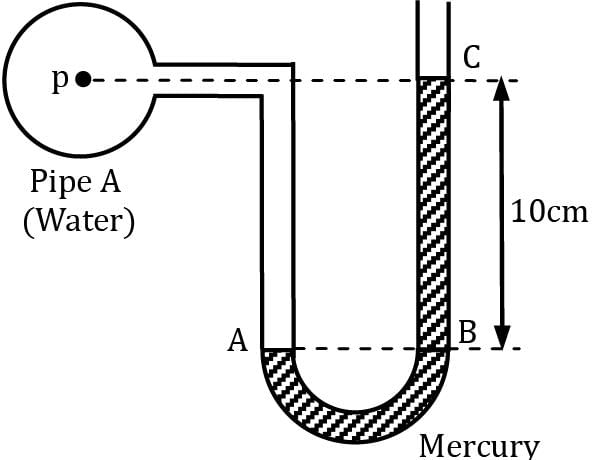
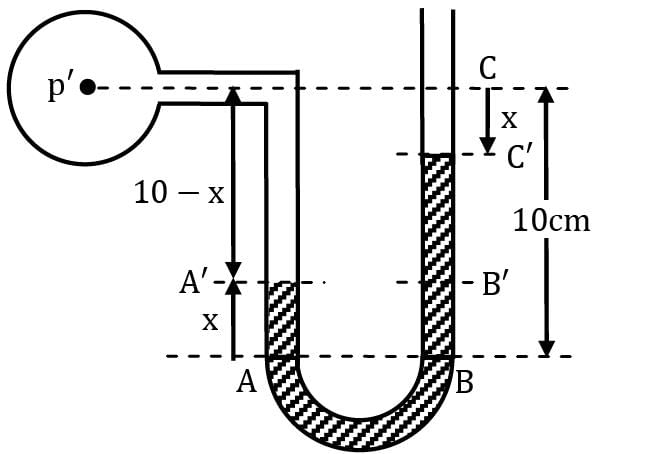
Find out the value of x?
Manometric fluid is mercury
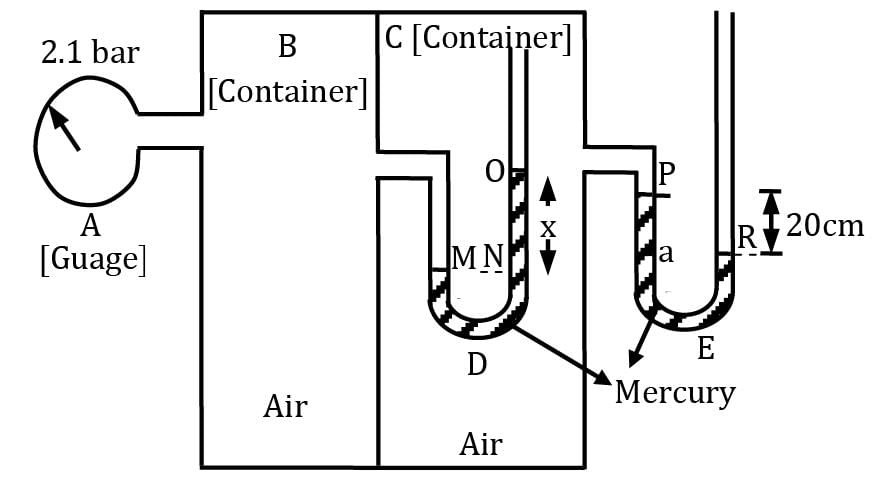
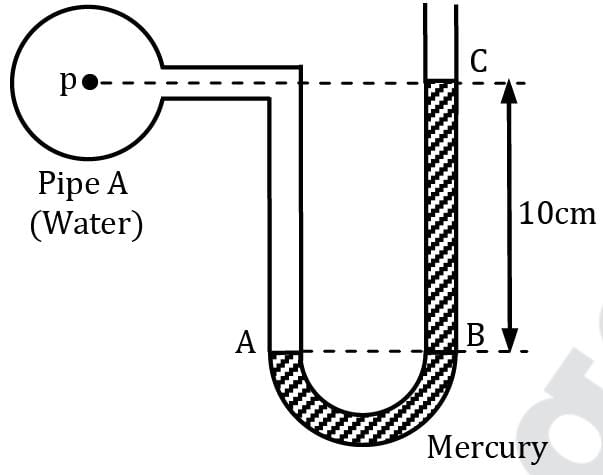
Consider the given configuration, if the pressure in pipe A reduces by 5 kN/m2, find out the new manometric height.
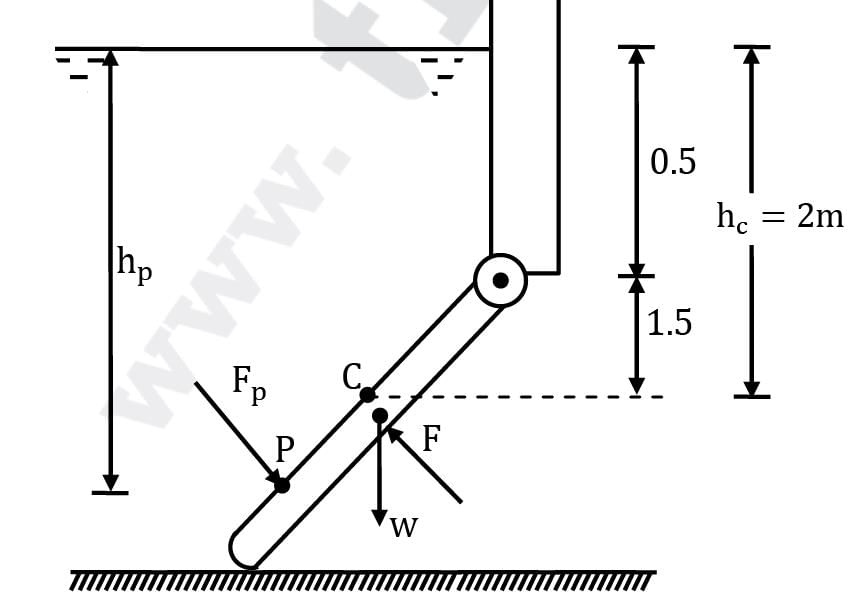
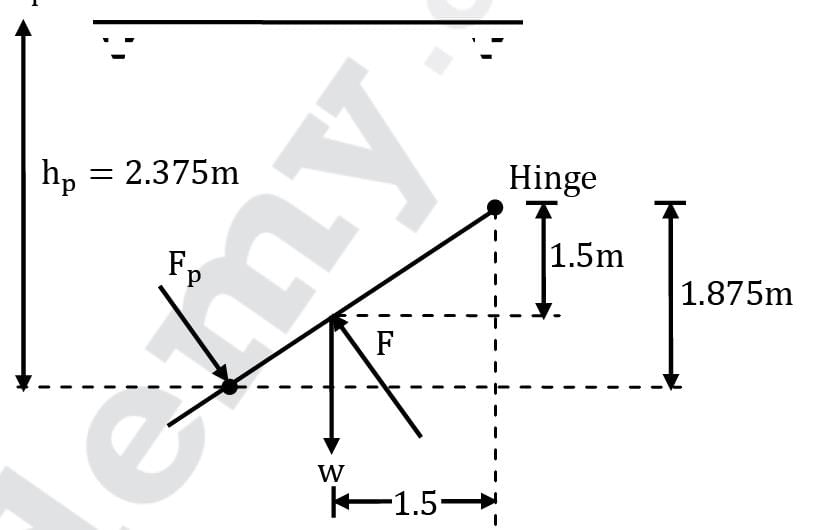
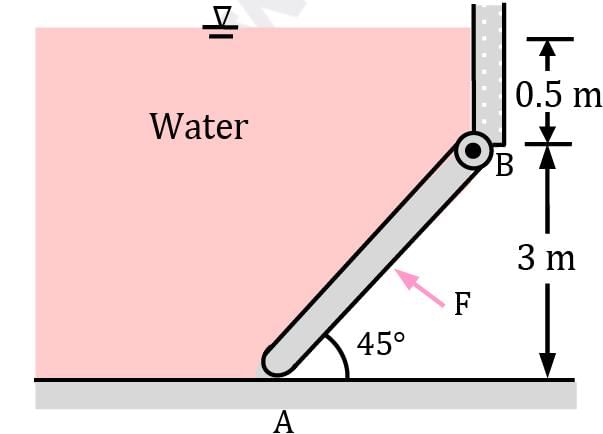
The 200-kg, 5-m-wide rectangular gate shown in figure is hinged at B and leans against the floor at A making an angle of 45° with the horizontal. The gate is to be opened from its lower edge by applying a normal force at its center. Determine the minimum force F required to open the water gate.
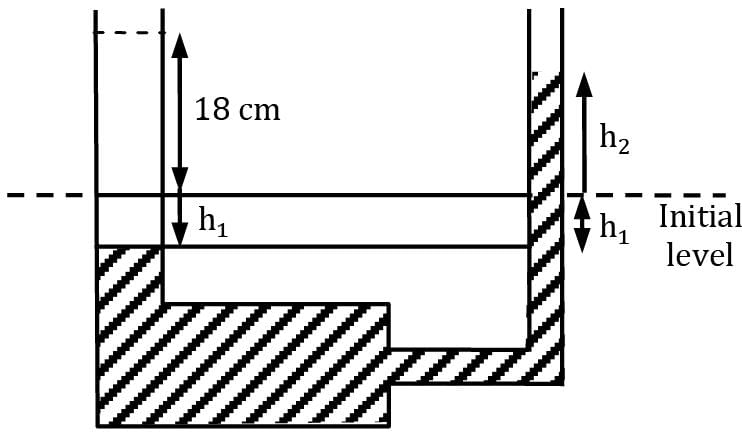
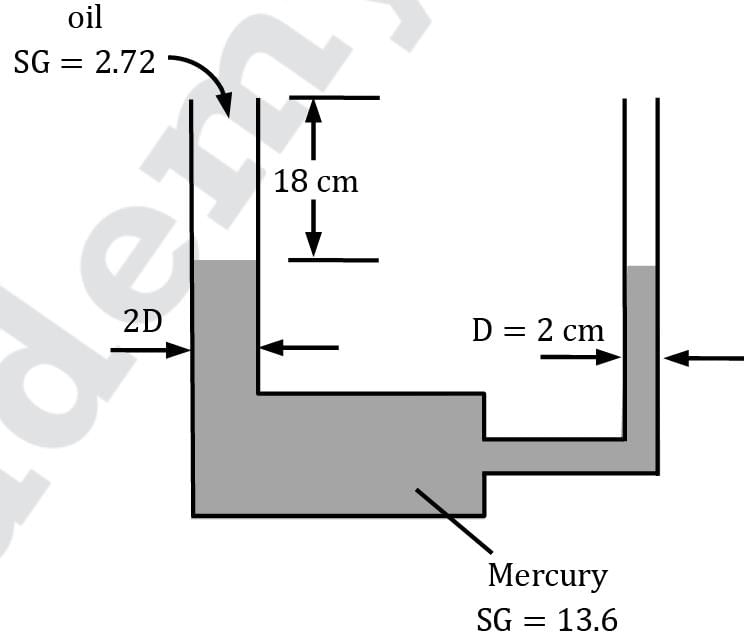
Consider a U-tube filled with mercury except the 18-cm-high portion at the top, as shown in figure. The diameter of the right arm of theU-tube is D = 2 cm, and the diameter of the left arm is 2D. Oil with a specific gravity of 2.72 is poured into the left arm, forcing some mercury from the left arm into the right one. Determine the maximum amount of oil in liters that can be added into the left arm.
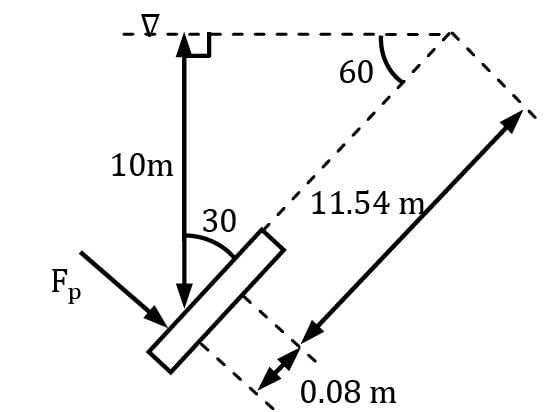
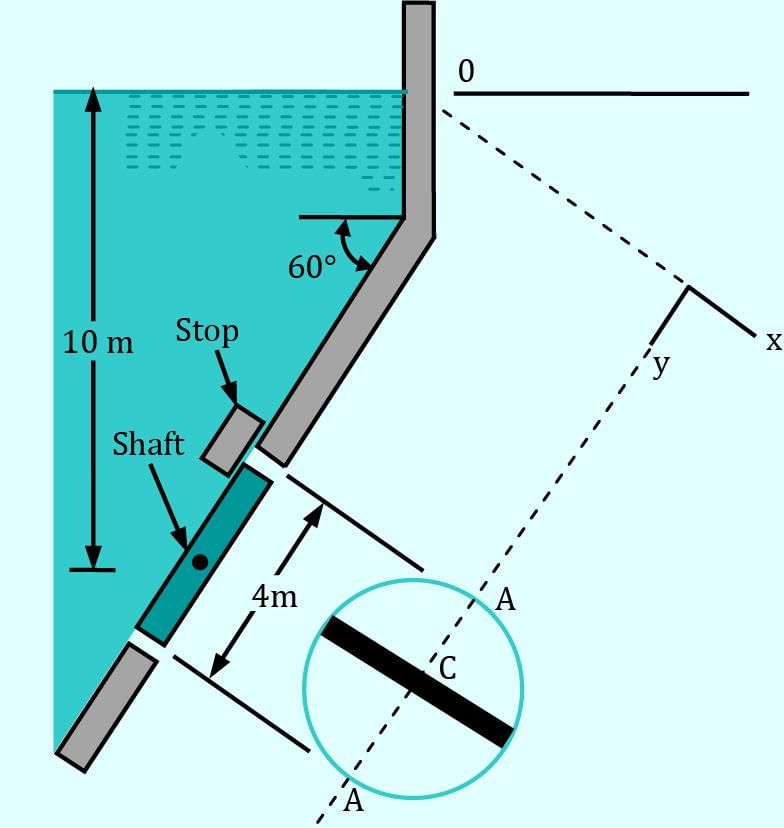
The 4-m–diameter circular gate of the figure is located in the incline wall of a large reservoir containing water (γ = 9.80 kN/m3). The gate is mounted on a shaft along its horizontal diameter, and the water depth is 10 m above the shaft. Determine the moment in kN-m that would have to be applied to the shaft to open the gate.
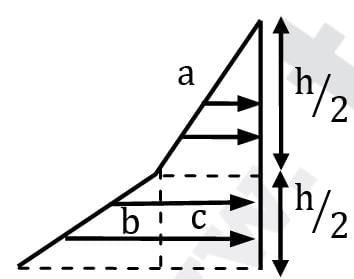
Consider a cuboidal tank of dimensions 20 cm × 20 cm × 20 cm. Two immiscible liquids (S1 = 1.2, S3 = 1.4), equal amount of each are poured into the container. Find the hydrostatic force on any of the side surfaces of the container and the depth of corresponding center of pressure.
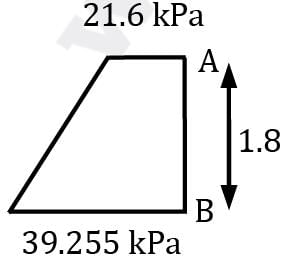
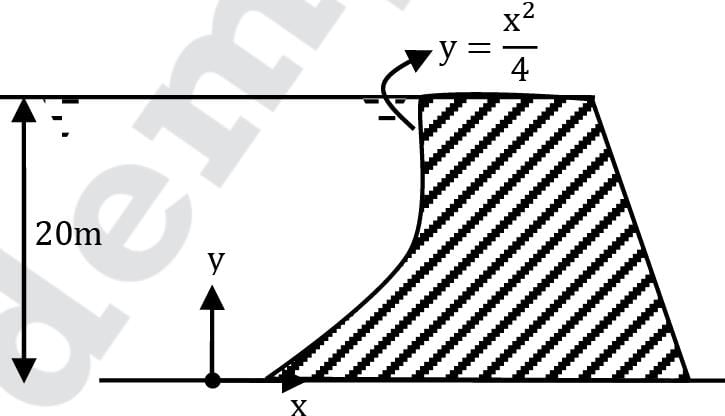
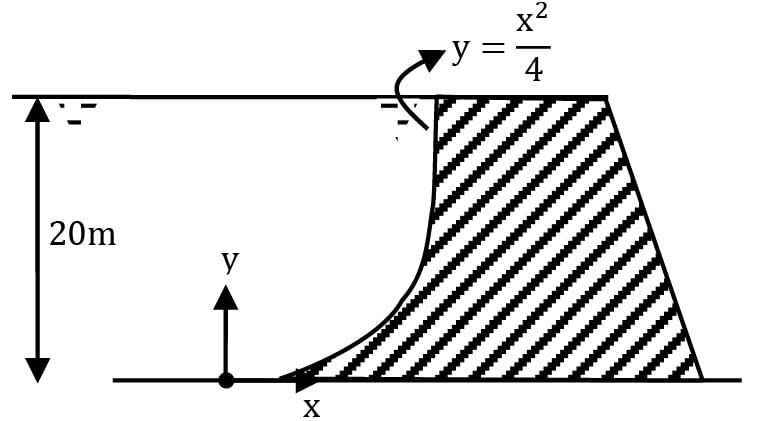
A dam is having a curved surface as shown in the figure. The height of the water retained by the dam is 20 m, density of water is 1000 kg/m3. Assuming g as 9.81 m/s2, the vertical force in kN acting on the dam per unit length is
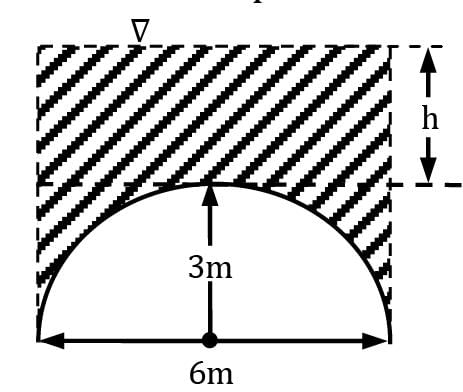
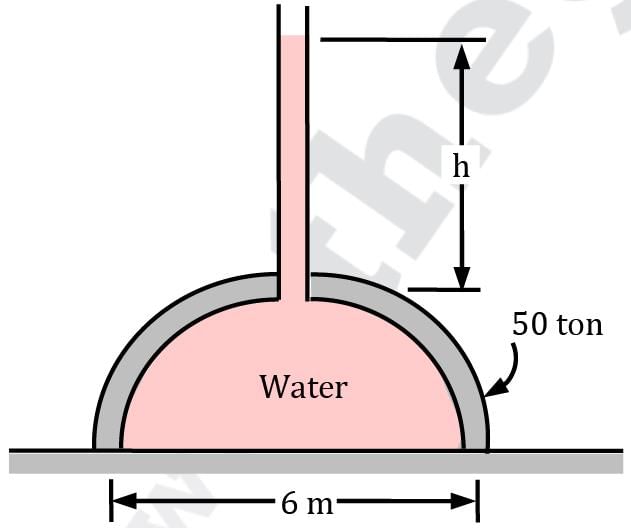
A 50-ton, 6-m-diameter hemispherical dome on a level surface is filled with water, as shown in figure. Someone claims that he can lift this dome by making use of Pascal’s law by attaching a long tube to the top and filling it with water. Determine the required height of water in the tube to lift the dome. Disregard the weight of the tube and the water in it.
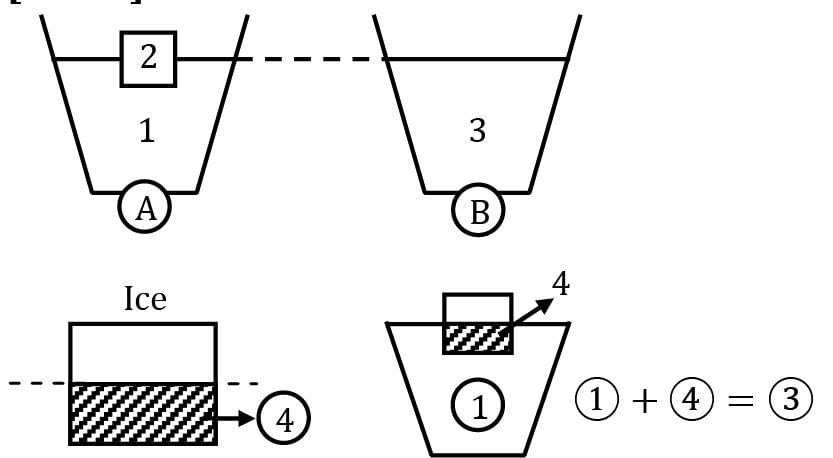
Common Data for Question No. 14 & 15 Consider two tumblers, A & B, initially empty. An ice block is placed in one of the tumblers, say A. Now slowly pour water in both the tumblers, such that the final water level is the same in the two.
As the ice in tumbler A melts, in which tumbler level will be more?
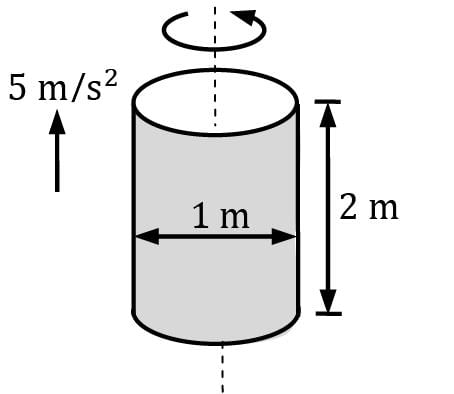
A 1-m-diameter, 2-m-high vertical cylinder is completely filled with gasoline whose density is 740 kg/m3. The tank is now rotated about its vertical axis at a rate of 90 rpm, while being accelerated upward at 5 m/s2. Determine
(i) the difference between the pressure at the centers of the bottom and top surfaces
(ii) the difference between the pressures at the center and the edge of the bottom surface.
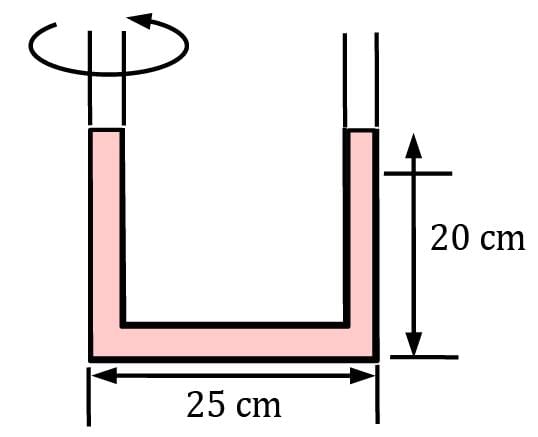
The distance between the centers of the two arms of a U-tube open to the atmosphere is 25 cm, and the U-tube contains 20-cm-high alcohol in both arms. Now the U-tube is rotated about the left arm at 4.2 rad/s. Determine the elevation difference between the fluid surfaces in the two arms.
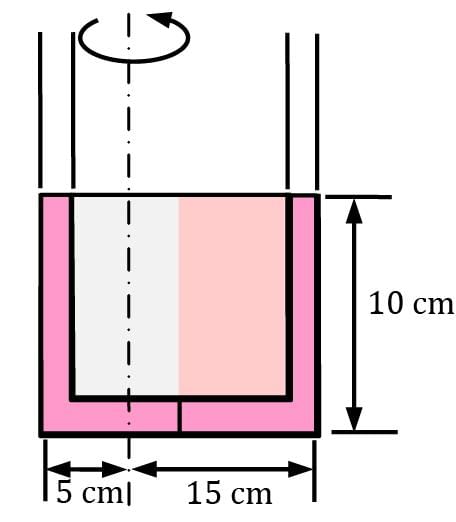
A U-tube contains water in the right arm, and another liquid in the left arm. It is observed that when the U–tube rotates at 30 rpm about an axis that is 15 cm from the right arm and 5 cm from the left arm, the liquid levels in both arms become the same. Determine the density of the fluid in the left arm.
A circular cylinder partly filled with a liquid is rotated about its axis at ω rad/s without spilling. At the walls, the rise of liquid surface above the original level will be
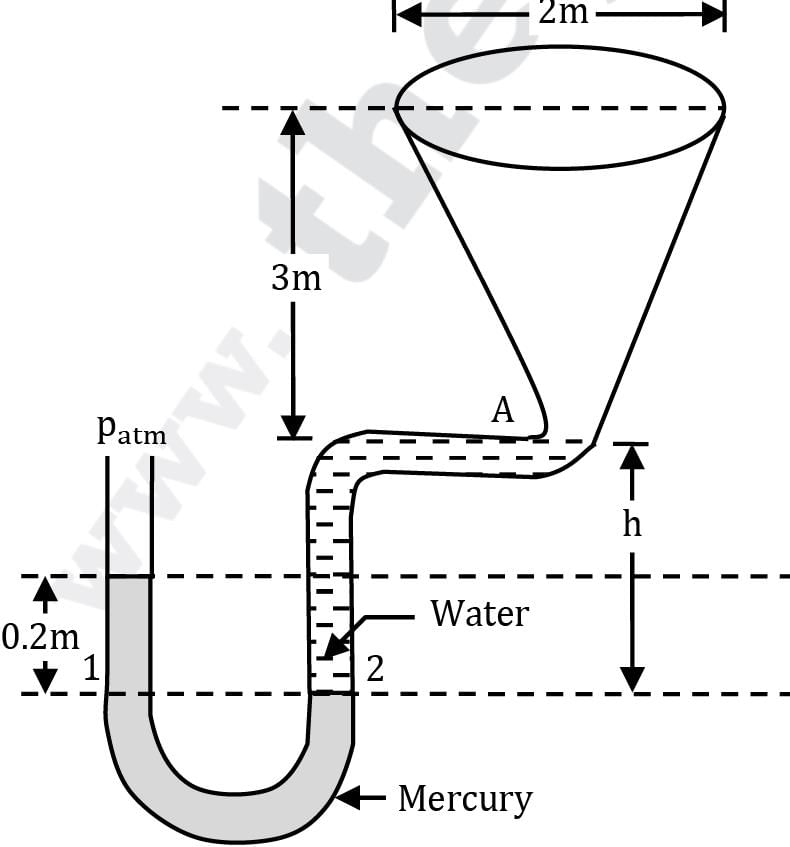
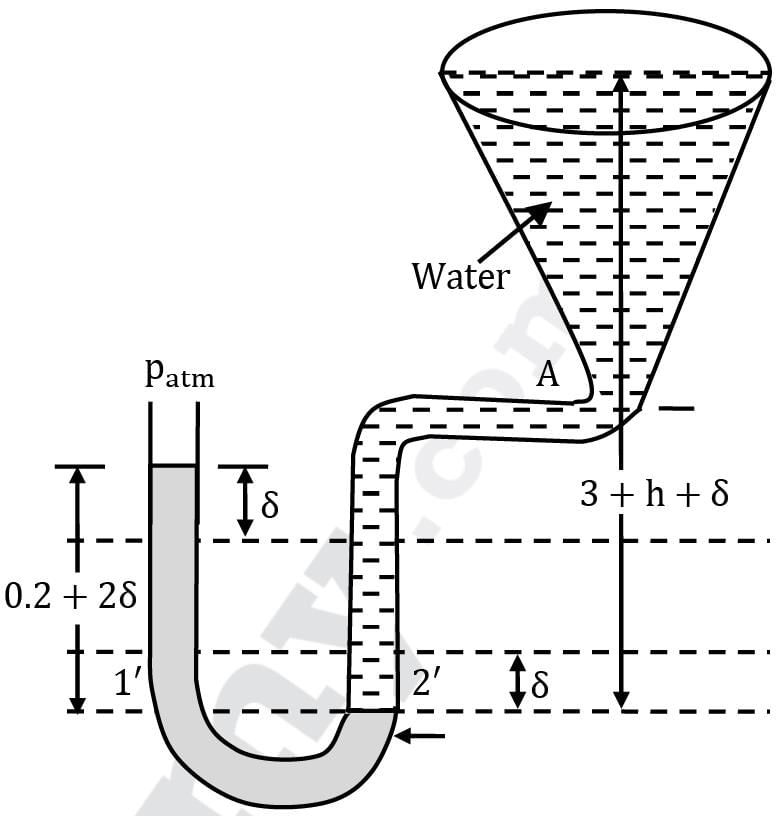
Figure shows a conical vessel having its outlet at A to which a U-tube manometer is connected. The reading of the manometer indicated in the figure pertains to the situation when the vessel is empty, i.e. the water surface is at A. Find the reading of the manometer when the vessel is completely filled with water.