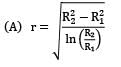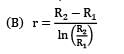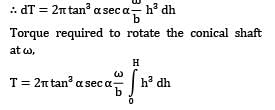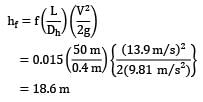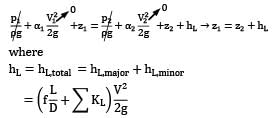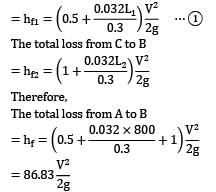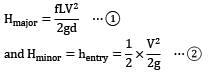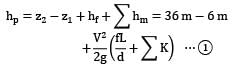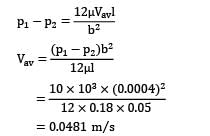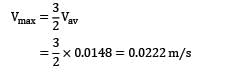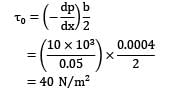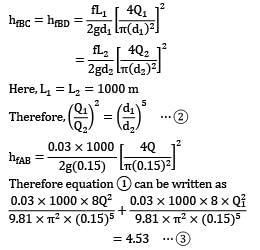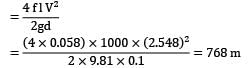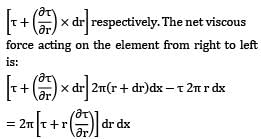All Courses
Get the App Signup / Login
Sign in Open App
Mechanical Engineering Exam  >  Mechanical Engineering Tests  >  Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Mechanical Engineering MCQ

Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Mechanical Engineering MCQ


Test Description

20 Questions MCQ Test - Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3

Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 for Mechanical Engineering 2024 is part of Mechanical Engineering preparation. The Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 questions and answers have been prepared according to the Mechanical Engineering exam syllabus.The Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 MCQs are made for Mechanical Engineering 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 below.
Solutions of Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 questions in English are available as part of our course for Mechanical Engineering & Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 solutions in Hindi for Mechanical Engineering course. Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free. Attempt Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 | 20 questions in 60 minutes | Mock test for Mechanical Engineering preparation | Free important questions MCQ to study for Mechanical Engineering Exam | Download free PDF with solutions
Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 1
Save

For a conical bearing, 100 watt power gets dissipated when a shaft with maximum cone radius 10 cm turns with 600 rpm over a uniform fluid layer of thickness 0.1 cm. If semi-angle for the conical bearing is 30°, make calculations for the dynamic viscosity of the fluid (in SI units).


Detailed Solution for Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 1
Consider an elementary ring of bearing surface of radius r and thickness dh at a distance h from the cone apex. Then r = h tan α and bearing area of the elementary ring equals dA = 2πr (dh sec α)

= 2πh tan α dh sec α

Viscous shear stress,

Since the shaft has an angular velocity ω, The tangential velocity, u = ωr = ωh tan α

∴ Viscous shear stress,

Tangential resistance on the ring, dF = shear stress × area of the ring

Torque = moment of tangential resistance = dF × r = dF × h tan α

Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 2
Save

Air (T = 20°C and p = 101kPa absolute) flows at a rate of 2.5 m3⁄s in a horizontal, commercial steel, HVAC duct of 0.3 m × 0.6 m. (Note that HVAC is an acronym for heating, ventilating, and air conditioning.) What is the pressure drop in mm of water per 50 m of duct? (Darcy friction factor, f = 0.015)


Detailed Solution for Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 2
1. Pressure drop due to head loss (hL)

p1 − p2 = ρghL

= 368,000

Thus, flow is turbulent. · Resistance coefficient: f = 0.015

3. Darcy-Weisbach equation

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 3
Save

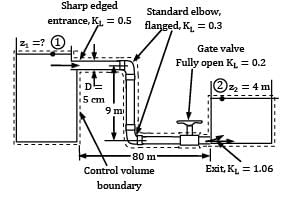
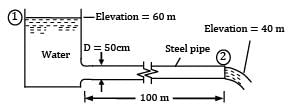
Water at 10°C flows from a large reservoir to a smaller one through a 5-cm-diameter cast iron piping system, as shown in Fig. Determine the elevation z1 (in m) for a flow rate of 6 L/s.

The density and dynamic viscosity of water at 10° C are ρ = 999.7 kg⁄m3 and μ = 1.307 × 10−3 kg⁄m ∙ s. The coefficient of friction = 0.0315.


Detailed Solution for Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 3
The density and dynamic viscosity of water at 10° C are ρ = 999.7 kg⁄m3 and μ = 1.307 × 10−3 kg⁄m ∙ s.

The piping system involves 89 m of piping, a sharp-edged entrance (KL = 0.5), two standard flanged elbows (KL = 0.3 each), a fully open gate valve (KL = 0.2), and a submerged exit (KL = 1.06). We choose points 1 and 2 at the free surfaces of the two reservoirs. Noting that the fluid at both points is open to the atmosphere (and thus p1 = p2 = patm ) and that the fluid velocities at both points are zero (V1 = V2 = 0), the energy equation for a control volume between these two points simplifies to

Since the diameter of the piping system is constant. The average velocity in the pipe and the Reynolds number are

Therefore, the free surface of the first reservoir must be 31.9 m above the ground level to ensure water flow between the two reservoirs at the specified rate.

Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 4
Save

Oil having a specific gravity of 0.8 and a viscosity of 2 × 10−2 N ∙ s/m2 flows downward between two vertical smooth plates spaced 10 mm apart. If the discharge per meter of width is 0.01 m2⁄s, what is the pressure gradient dp⁄ds for this flow? Give your answer in kPa/m.

Detailed Solution for Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 4

Note: The pressure increases in the downward direction which means that the pressure, in part, supports the weight of the fluid.

Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 5
Save

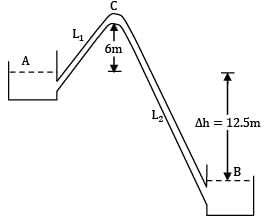
Two reservoirs open to the atmosphere are connected by a pipe 800 metres long. The pipe goes over a hill whose height is 6 m above the level of water in the upper reservoir. The pipe diameter is 300 mm and friction factor f = 0.032. The difference in water levels in the two reservoirs is 12.5 m. If the absolute pressure of water anywhere in the pipe is not allowed to fall below 1.2 m of water in order to prevent vapour formation, calculate the length of pipe in the portion between the upper reservoir and the hill summit. Neglect bend losses.

Detailed Solution for Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 5

Let the length of pipe upstream of C be L1 and that of the downstream be L2 It is given L1 + L2 = 800 m Considering the entry, friction and exit losses, The total loss from A to C

Applying Bernoulli’s equation between ! and B, we have

Δ H = hf

which gives hf1 = 2.99 m Using the value of hf1 = 2.99 m, and V = 1.68 m/s in equation ① we get

Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 6
Save

Water (T = 20°C) flows from a tank through a 50 cm diameter steel pipe. Determine the discharge of water in m3/s. (Friction factor = 0.012)

Properties: 1. Water at 20°C, ν = 1 × 10−6 m2⁄s 2. The Darcy friction factor = 0.012 Also consider all possible losses in the flow.

Detailed Solution for Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 6
All the possible losses will be major head loss and minor head loss

Note: Since water is flowing out into the atmosphere from ②; there will be no exit losses as exit loss occurs only when fluid flows from a pipe to a tank. Applying Bernoulli’s equation at ① and ②

Q = 1.96 m3/s

Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 7
Save

Water ρ = 1000 kg/m3and ν = 1.02 × 10−6 m2/s is pumped between two reservoirs at 5.66 × 10−2 m3/s through 122 m of 5.1 cm diameter pipe and several minor losses, as shown in Fig. Compute the pump power required in kW. f = 0.0216

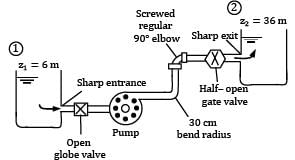
Loss K

Sharp entrance

Open globe valve

30 cm bend

Regular 90° elbow

Half-closed gate valve

Sharp exit

0.5

6.9

0.25

0.95

2.7

1.0


Detailed Solution for Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 7
Writing the steady flow energy equation between sections 1 and 2, the two reservoir surfaces

where hp is the head increase across the pump. But since p1 = p2 and V1 = V2 ≈ 0, solving for the pump head:

Now with the flow rate known, calculate

Now list and sum the minor loss coefficients: The Reynolds number is

f = 0.0216. Substitute into Equation ①

= 30 m + 25 m = 55 m Pump head

The pump must provide a power to the water of

P = ρgQhp = 1000 × 9.81 × 0.00566 × 55 = 3.054 kW

Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 8
Save

An oil with a viscosity of μ = 0.40 N ∙ s⁄m2 and density ρ = 900 kg⁄m3 flows in a pipe of diameter D = 0.020 m.

(i) What pressure drop, p1 − p2 , is needed to produce a flow rate of Q = 2.0 × 10−5 m3⁄s if the pipe is horizontal with x1 = 0 and x2 = 10 m?

(ii) How steep a hill, θ must the pipe be on if the oil is to flow through the pipe at the same rate as in part (a), but with p1 = p2?
Detailed Solution for Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 8
(a) If the Reynolds number is less than 2100 the flow is laminar and the equations derived in this section are valid. since the average velocity is

or Δp = 20,400 N/m2 = 20.4 kPa

Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 9
Save

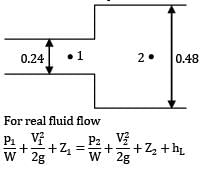
A sudden enlargement of a water pipeline from a diameter of 0.24 m to 0.48 m. The HGL rises by 10 mm. Then find the discharge in m3/s.

Detailed Solution for Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 9
From Bernoulli’s equation

Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 10
Save

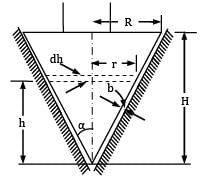
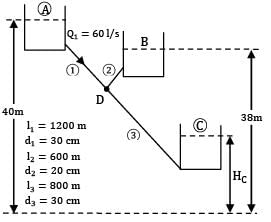
Three reservoirs A, B and C are connected by a pipe system as shown in figure. The height of water level in reservoir C is __________ m. Take f = 0.024 for all pipes.

Detailed Solution for Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 10
Applying Bernoulli’s equation between ! and D, we have,

Hence HB > HD; hence flow will be from B to D Applying Bernoulli’s equation between, B and D we have,

⇒ HC = 36.44 − 4.26

⇒ HC = 32.2 m

Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 11
Save

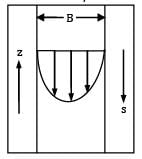
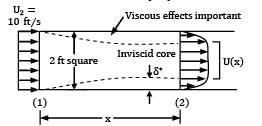
Air flowing into a 2-ft–square duct with a uniform velocity of 10 ft/s forms a boundary layer on the walls as shown in Fig. The fluid within the core region (outside the boundary layers) flows as if it were inviscid. From advanced calculations it is determined that for this flow the boundary layer displacement thickness is given by δ∗ = 0.0070(x)1⁄2 where δ∗ and x are in feet. Determine the velocity U = U(x) of the air within the duct but outside of the boundary layer.

Detailed Solution for Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 11
If we assume incompressible flow (a reasonable assumption because of the low velocities involved), it follows that the volume flowrate across any section of the duct is equal to that at the entrance (i. e. , Q1 = Q2). That is,

According to the definition of the displacement thickness, δ∗, the flowrate across section (2) is the same as that for a uniform flow with velocity U through a duct whose walls have been moved inward by δ∗. That is,

By combining Equations (1) and (2) we obtain

Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 12
Save

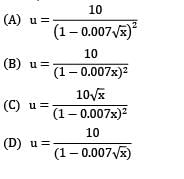
A container full of oil has a horizontal parallel crack in its end wall which is 500 mm wide and 50 mm thick in the direction of flow. The pressure difference between two faces of the crack is 10 kPa and the crack forms a gap of 0.4 mm between the parallel surfaces.

Calculate

(i) Maximum leakage velocity;

(ii) Shear stress at the boundary.

Take specific gravity and viscosity of oil equal to 0.85 and 1.8 poise respectively.
Detailed Solution for Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 12
μ = 1.8 poise = 1.8 × 0.1 = 0.18 Ns⁄m2

b = 0.4 mm = 0.0004 m

l = 50 mm = 0.05 m

p1 − p2 = 10 kPa = 10 × 103 N⁄m2

(i) The oil leakage through the crack corresponds to the case of flow between two stationary parallel surfaces for which

(ii) The maximum velocity occurs midway between the crack

Shear stress at the wall,

Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 13
Save

A spindle 5 cm in diameter turns 110 revolutions per minute in a bearing 5.004 cm internal diameter. The intervening space is filled to 20 cm depth with a lubricating oil of dynamic viscosity 0.08 Pa‑s. If the oil pressure is 4000 kPa, make calculations for the oil leakage along the spindle and the resisting torque due to viscous drag of the oil film.
Detailed Solution for Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 13
Given μ = 0.08 Pa‑s = 0.08 Ns⁄m2 radial clearance,

∴ Oil leakage = clearance area × average velocity

= π db × Vav = π × 0.05 × 0.2 × 10−4 × 0.00833 = 2.61 × 10−8 m3⁄s

Shear stress,

where ω is the angular velocity and r is the radius of the spindle. Viscous torque

= viscous force × radial distance

= (shear stress × area) × radius

Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 14
Save

Determine the amount of flow (in m3 /s) per meter width between two parallel plates when one is moving relative to the other with a velocity of 3 m/s in the negative x-direction, if dp /dx = −100 N⁄cm2 /cm, μ is 0.4 poise and the distance between the plates is 1 mm.

Detailed Solution for Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 14
For laminar flow between parallel plates having relative motion (lower plate fixed and the upper plate moving uniformly with velocity V), the velocity distribution is given by

The discharge is in the positive x-direction, i.e., in the direction opposite to that of moving plate.

Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 15
Save

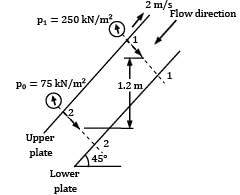
Laminar flow of a fluid of viscosity 0.90 kg⁄ms and mass density 1250 kg⁄m3 occurs between a pair of plates of extensive width; the plates are 10 mm apart and are inclined at 45 degree to the horizontal. Pressure gauges mounted at two points 1.2 m vertically apart on the upper plate record pressure of 75 kN⁄m2 and 250 kN⁄m2 at the lower and upper point respectively. The upper plate moves with a velocity of 2.0 m⁄s relative to the lower plate but in a direction opposite the fluid flow. Make calculations for (i) the maximum flow velocity, and (ii) the shear stress on the upper plate.
Detailed Solution for Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 15
Since the plates are placed uniformly apart, velocity head would be the same at the two sections and as such flow direction will be dictated by the value of the piezometric head.

Taking a horizontal line passing through point 2 as datum Piezometric head at point 1,

p1∗ = p1 + wy1

Since p1∗ is greater that p2∗ , the direction of flow is from section 1-1 to section 2-2, i.e., downward. Apparently the upper plate is moved up the slope. Pressure gradient

Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 16
Save

Two reservoirs are connected through a 300 mm diameter pipe line, 1000 m long as shown in figure. At a point B, 300 m from reservoir A, a valve is inserted on a short branch line which discharges to the atmosphere. The valve may be regarded as a rounded orifice 75 mm diameter, Cd = 0.65. If friction factor f for all the pipes is 0.013. Estimate the leakage through the short pipe line at B (in m3/s).

Detailed Solution for Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 16
Let the flow rate through the first 300 m of the pipe be Q and the flow rates through the next 700 m of the pipe and the short branch line containing the valve be Q1 and Q2 respectively.

From continuity, Q = Q1 + Q2

The discharge through the valve acting as an orifice can be written as

Using equation ① and ②, we have

= 0.224 Q1

Hence, Q = 1.224 Q1

Applying Bernoulli’s equation between A and C through the path ABC, we have,

which gives Q1 = 0.231 m3/s

Q2 = 0.224 × 0.231 = 0.052 m3/s

Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 17
Save

A pipeline conveys 8.23 litre per second of water from an overhead tank to a building. The pipe is 2 km long and 0.15 m in diameter. It is desired to increase the discharge by 30% by installing another pipeline in parallel with this over half the length. Suggest a suitable diameter of the pipe to be installed. Is there any upper limit on discharge augmentation by this arrangement? (Take friction factor f = 0.03. )
Detailed Solution for Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 17
The height H of the overhead tank above the building can be determined from the conditions with a single pipe.

d = 0.15 m

l = 2 km

f = 0.03

In the new plan as shown in figure hf = 4.53 = hfAB + hfBC ⋯ ① again,

In this case, Q = 1.3 × 0.00833 = 0.0108 m3/s Then, from equation ③, we get

Q12 = 0.00014 − (0.0108)2

which gives Q1 = 0.0048 m3/s From continuity,

Q2 = 0.0108 − 0.0048

= 0.006 m3/s

From equation ②, we have

?2 = 0.1?? ?

It can be observed from equation ③ that

Q12 = 0.00014 − Q2

or Q2 = 0.00014 − Q21

Now, Q will be maximum when Q1 will be minimum. For a physically possible situation, the minimum value of Q1 will be zero. Therefore, the maximum value of Q will be

Qmax = √0.00014 = 0.0118 m3/s which is 41.6% more than the initial value. The case (Q1 = 0, Q = 0.0118 m3/s) corresponds to a situation of an infinitely large branched pipe, i.e. d2 → ∞.

Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 18
Save

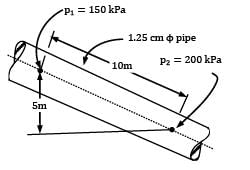
A liquid of dynamic viscosity 0.04 Pa s and specific weight 8 kN⁄m3 is being pumped through a pipe of 1.25 cm diameter laid on slope as shown in Fig. For the pressures indicated, work out the direction and rate of flow (in ml/s) through the pipe.

Detailed Solution for Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 18
Since the pipe is of uniform diameter, velocity head would be the same at the two sections and as such flow direction will be dictated by the values of the piezometric head. Taking a horizontal line passing through point 2 as the datum, then

p1∗ = p1 + wy1

= 150 + (8 × 5) = 190 kPa

p2∗ = p2 + wy2

= 200 + (8 × 0) = 200 kPa

Since p2∗ is greater then p1∗ , the direction of flow is from point 2 to point 1.

Using the Hagen–Poiseuille law,

Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 19
Save

A pipe 10 cm in diameter and 1000 m long is used to pump oil of viscosity 3.5 poise and specific gravity 0.92 at the rate of 1200 litre/min. The first 300 m of the pipe is laid along the ground sloping upwards at 10° to the horizontal and the remaining pipe is laid to the ground sloping upwards at 15° to the horizontal. Determine the power (in kW) of the driving motor if the pump efficiency is 60 percent. Assume suitable data for friction coefficient f, if required.

Detailed Solution for Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 19
Discharge, Q = 1200 litre⁄min

Viscosity, μ = 8.5 poise = 8.5 × 0.1 = 0.85 N s⁄m

Flow velocity = discharge / area

= 275.78

Since the Reynolds number is less than 2000, the flow is laminar. For laminar flow, the friction coefficient is given by

Head loss due to friction in 1000 m length of pipe

The pressure to be developed by the pump can be worked out by applying Bernoulli’s equation between the pump outlet (suffix 1) and the end of the pipeline (suffix 2)

With horizontal line through the pump center,

y1 = 0

and y2 = 300 sin 10° + 700 sin 15° = 233.25 m p2 = 0 as the pressure at the pipe exit is atmospheric Also V1 = V2

∴p1 / w = 233.25 + 768

= 1001.25 m of oil

Power required to develop this pressure

= w Q H

= (0.92 × 1000 × 9.81) × 0.02 × 1001.25

= 180729 Nm⁄s ≈ 180.73 kW

Power of driving motor

Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 20
Save

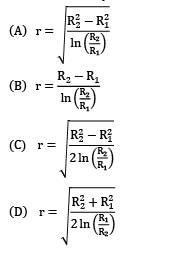
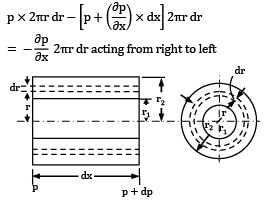
A circular pipe of radius R1 is placed concentrically inside another pipe of radius R2. If the flow in the annular space between the pipes is laminar. Find the r where maximum velocity occurs.

Detailed Solution for Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 - Question 20
Consider an annular element of radius r, thickness dr and length dx. Further let the velocity at radius r be u and pressure at two sections dx apart be p and

Force on the element due to pressure difference is,

Figure flow through an annular space Let shear stresses on the inner and outer surfaces of the element be τ and

Since the fluid is not accelerating (i.e., is moving with constant velocity), the sum of the pressure and viscous forces acting on the element must be zero. Thus:

Local velocity u would be maximum when

Information about Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 Page
In this test you can find the Exam questions for Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Viscous Flow of Incompressible Fluids, Flow Losses Level - 3, EduRev gives you an ample number of Online tests for practice

Top Courses for Mechanical Engineering

Download as PDF

Top Courses for Mechanical Engineering

Important Questions for Viscous Flow of Incompressible Fluids, Flow Losses Level - 3

Find all the important questions for Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 at EduRev.Get fully prepared for Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 resources.

Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 MCQs with Answers

Prepare for the Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 within the Mechanical Engineering exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Viscous Flow of Incompressible Fluids, Flow Losses Level - 3

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Viscous Flow of Incompressible Fluids, Flow Losses Level - 3 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup