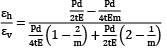All Courses
Get the App Signup / Login
Sign in Open App
Mechanical Engineering Exam  >  Mechanical Engineering Tests  >  Test: Thin Cylinder Level - 2 - Mechanical Engineering MCQ

Test: Thin Cylinder Level - 2 - Mechanical Engineering MCQ


Test Description

10 Questions MCQ Test - Test: Thin Cylinder Level - 2

Test: Thin Cylinder Level - 2 for Mechanical Engineering 2024 is part of Mechanical Engineering preparation. The Test: Thin Cylinder Level - 2 questions and answers have been prepared according to the Mechanical Engineering exam syllabus.The Test: Thin Cylinder Level - 2 MCQs are made for Mechanical Engineering 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Thin Cylinder Level - 2 below.
Solutions of Test: Thin Cylinder Level - 2 questions in English are available as part of our course for Mechanical Engineering & Test: Thin Cylinder Level - 2 solutions in Hindi for Mechanical Engineering course. Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free. Attempt Test: Thin Cylinder Level - 2 | 10 questions in 30 minutes | Mock test for Mechanical Engineering preparation | Free important questions MCQ to study for Mechanical Engineering Exam | Download free PDF with solutions
Test: Thin Cylinder Level - 2 - Question 1
Save

A thin cylindrical vessel closed at both ends is subjected to fluid pressure resulting in a hoop stress of 24 N/mm2. The maximum shear stress in the cylinder is

Detailed Solution for Test: Thin Cylinder Level - 2 - Question 1

= 6

Test: Thin Cylinder Level - 2 - Question 2
Save

A 600 mm diameter pipe contains a fluid at a pressure of 3 N/mm2. If the safe stress in tension is 75 N/mm2, the minimum thickness of pipe is equal to

Detailed Solution for Test: Thin Cylinder Level - 2 - Question 2
Diameter, d = 600mm Pressure,

P = 3 N/mm2 Safe

streee = 75 N/mm2 Minimum thickness, t =?

75 =

t = 12mm

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: Thin Cylinder Level - 2 - Question 3
Save

In a thin cylinder, hoop stress is 48 N/mm2. The max. Shear stress developed in the pipe material is

Detailed Solution for Test: Thin Cylinder Level - 2 - Question 3
σh = 48 N/mm2 , σlongitudinal = σl = 24 N/mm2

Max shear stress,

=12N/mm2

Test: Thin Cylinder Level - 2 - Question 4
Save

A cylinder of internal diameter 2.5m and of thickness 5cm contains a gas. If the tensile stress in the material is not to exceed 80 N/mm2, the internal pressure of the gas should be
Detailed Solution for Test: Thin Cylinder Level - 2 - Question 4

80 =

P= 3.2 N/mm2

Test: Thin Cylinder Level - 2 - Question 5
Save

A pressure vessel in the form of a thin cylinder of 1 m diameter and 1mm plate thickness is subjected to an internal fluid pressure of 0.2MPa. The maximum shear stress in the material is
Detailed Solution for Test: Thin Cylinder Level - 2 - Question 5
d = 1 m = 103 mm t = 1 mm P = 0.2 MPa

τmax =

= 50 MPa

Test: Thin Cylinder Level - 2 - Question 6
Save

A cylinder of thickness 1.5cm has to withstand maximum internal pressure of 1.5 N/mm2. If the ultimate tensile stress in the material of the cylinder is 300 N/mm2, factor of safety 3.0 and joint efficiency 80%, the diameter of the cylinder is
Detailed Solution for Test: Thin Cylinder Level - 2 - Question 6

300/3 =

d = 1600 mm = 160 cm

Test: Thin Cylinder Level - 2 - Question 7
Save

In case of thin walled cylinder the ratio of hoop strain to Volumetric strain is
Detailed Solution for Test: Thin Cylinder Level - 2 - Question 7
Hoop strain,

εh =

Longitudinal strain,

εl =

=

Volumetric strain,

εv = εl + 2εb

=

=

εv=

=

=

Test: Thin Cylinder Level - 2 - Question 8
Save

A thin cylindrical shell of diameter ‘d’, length ‘l’ and thickness ‘t’ is subjected to an internal pressure ‘p’. What is the ratio of longitudinal strain to hoop strain in terms of Poisson’s ratio (1/m)?
Detailed Solution for Test: Thin Cylinder Level - 2 - Question 8
For a thin cylinder, longitudinal strain,

εl =

Now,

Test: Thin Cylinder Level - 2 - Question 9
Save

A cylindrical steel pressure vessel 400mm in diameter with a wall thickness of 20mm is subjected to an internal pressure of 4.5 MPa. Calculate the circumferential stresses (σx ) and longitudinal stresses (σy ) in the steel vessel.
Detailed Solution for Test: Thin Cylinder Level - 2 - Question 9
Diameter = 400mm t = 20mm

p = 4.5 MPa

Circumferential stresses,

σx =

σx = 45 MPa

Longitudinal stresses,

σy =

σy = 22.5 MPa

Test: Thin Cylinder Level - 2 - Question 10
Save

A water tank, 7000 mm in diameter, is made from steel plates that are 15 mm. thick. Find the maximum height to which the tank may be filled if the circumferential stress is limited to 40 MPa. The specific weight of water is 9800 N/m3
Detailed Solution for Test: Thin Cylinder Level - 2 - Question 10
Diameter = 7000 mm t = 15mm Pressure of water = rh = 9800 h N/m2

Maximum circumferential stress,

= = 40 MPa

40 =

h = 8.75m × 2 = 17.5m

Information about Test: Thin Cylinder Level - 2 Page
In this test you can find the Exam questions for Test: Thin Cylinder Level - 2 solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Thin Cylinder Level - 2, EduRev gives you an ample number of Online tests for practice

Top Courses for Mechanical Engineering

Download as PDF

Top Courses for Mechanical Engineering

Important Questions for Thin Cylinder Level - 2

Find all the important questions for Thin Cylinder Level - 2 at EduRev.Get fully prepared for Thin Cylinder Level - 2 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Thin Cylinder Level - 2 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Thin Cylinder Level - 2 resources.

Thin Cylinder Level - 2 MCQs with Answers

Prepare for the Thin Cylinder Level - 2 within the Mechanical Engineering exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Thin Cylinder Level - 2

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Thin Cylinder Level - 2 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup