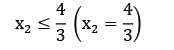Test: Linear Programming Level - 2 - Mechanical Engineering MCQ
20 Questions MCQ Test - Test: Linear Programming Level - 2
Consider the following linear programming problem:
Max. Z = 2A + 3B, subject to A + B < 10, 4A + 6B < 30, 2A + B < 17, A, B ≥ 0.
What can one say about the solution?
The solution for the LPP is
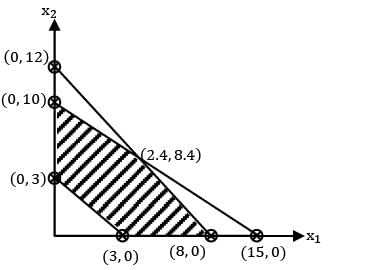
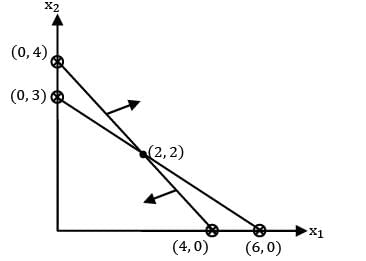
Max z = 3x1 + 2x2
s/t: 2x1 + 3x2 ≤ 30
3x1 + 2x2 ≤ 24
x1 + x2 ≥ 3
x1 , x2 ≥ 0
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
For a given LPP, Z = 50x1 + 25x2 (max) s/t: 2x1 + 3x2 ≤ 12
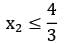
x1 , x2 ≥ 0
The type of solution obtained is
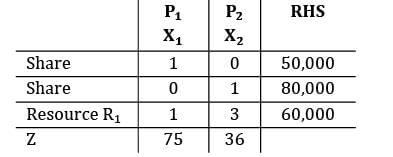
A company produces two products P1 and P2 . The profits per unit of P1 and P2 are Rs.75 and Rs.36 respectively. The market share of the company is 50,000 units of P1 and 80,000 units of P2 .The product P1 require one unit of resource R1 and P2 requires 3 units of resource R1 . The company has a maximum of 60,000 units of R1 . The constraint for resource R1 can be written as
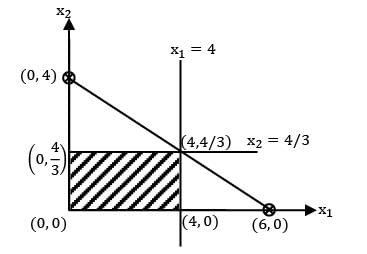
Min z = 4x1 + 6x2
s/t: x1 + x2 ≤ 4
x1 + 2x2 ≥ 6
x1, x2 ≥ 0
The type of solution is
Which of the following type of solution is not possible in simplex method?
Which of the following statements are true?
I. Simplex method can handle only ≤ type constraints
II. Simplex method can be applied only when the number of decision variables are ≥ 3
III. Simplex method can be applied to only maximization problems
In a transportation problem rows are the supply points and columns are the demand points. If total supply is less than total demand then
Which one of the following statements is NOT correct?
If the numbers of sources are 6 and the number of destinations are 7. The total number of non-redundant constraints in linear programming problem formulation is ___________
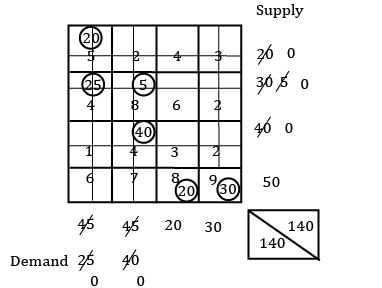
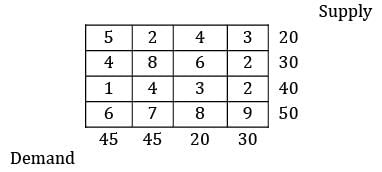
Consider the given problem. Find the total cost of transportation using N-W method.
In order for a transportation matrix which has six rows and four columns, not to be degenerate, how much must be the number of allocated cells in the matrix?
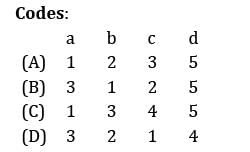
Match List-I (O.R. Techniques) with List-II (Application) and select the correct answer using the codes given below the lists:
In a 6 × 6 transportation problem, degeneracy would arise, if the number of filled slots were
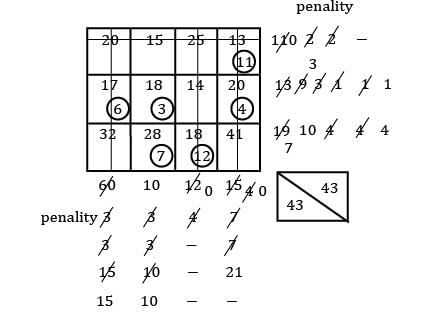
Determine the initial basic feasible solution of the following transportation problem by using VAM.
Consider the following statements: The assignment problem is seen to be the special case of the transportation problem in which
1. m = n
2. All ai = 1
3. xij = 1
(The symbols have usual meaning) Which of the statements given above are correct?
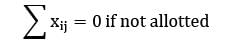
In an assignment problem having n facilities and n jobs, what is the number of possible ways of making assignments?
If there are two constraints in an LPP of which one of the constraints is redundant. The maximum possible number of corner points of the feasible region is
As one constraint is redundant it will not touch feasible region.
Consider the following statements regarding linear programming
1. Dual of a dual is the primal.
2. When two minimum ratios of the right hand side to the coefficient in the key column are equal, degeneracy may take place.
Select the correct answer from the codes given below
Codes:
Top Courses for Mechanical Engineering
Important Questions for Linear Programming Level - 2
Linear Programming Level - 2 MCQs with Answers
Online Tests for Linear Programming Level - 2
|
© EduRev
|
Education Revolution
|
Follow Us
|
