Test: Coordinate Geometry- 2 - CAT MCQ
10 Questions MCQ Test - Test: Coordinate Geometry- 2
Distance of a point from the origin:
The distance of a point A(x, y) from the origin O(0, 0) is given by OA = √x2 + y2
Find the distance of the point A(4, -2) from the origin.
Distance between two points :
If (x1, y1) and B(x2, y2) be two points, then AB = √(x2 - x1)2 + (y2 - y1)2
Find the distance between the points A(-4, 7) and B(2, -5).
The distance between the points A(b, 0) and B(0, a) is.
If the distance of the point P(x, y) from A(a, 0) is a + x, then y2 = ?
The distance between the points A(5, -7) and B(2, 3) is:
Area of a triangle :
If A(x1,y1), B(x2,y2 and C(x3, y3) be three vertices of a ΔABC, then its area is given by:
Δ = 1/2 [x1(y2 - y3 + x2(y3 - y1) + x3(y1 - y2)]
Find the area of ΔABC whose vertices are A(9, -5), B(3, 7) and (-2, 4).
Find the area of ΔABC whose vertices are A(2, -5), B(4, 9) and (6, -1).
The points A(0, 6), B(-5, 3) and C(3, 1) are the vertices of a triangle which is ?
The points A(-4, 0), B(1, -4), and C(5, 1) are the vertices of
Find the coordinates of the point equidistant from the points A(1, 2), B (3, –4) and C(5, –6).




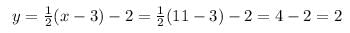
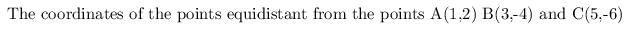 (11,2)
(11,2)















