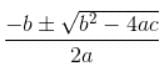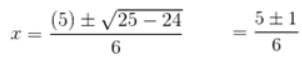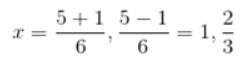Test: Quadratic Equations (Hard) - Class 10 MCQ
20 Questions MCQ Test - Test: Quadratic Equations (Hard)
The values of k for which the roots are real and equal of the following equation kx2 —
2√5x + 4 = 0 is k = 5/4
Which of the following is not quadratic equation?
If the sum of the roots of a quadratic equation is 5 and the product of the roots is also 5, then the equation is
A rectangular field has an area of 3 sq. units. The length is one more than twice the breadth ‘x’. Frame an equation to represent this.
If a train travelled 5 km/hr faster, it would take one hour less to travel 210 km. The speed of the train is :
If the solutions of the equation x2 + 3x − 18 = 0 are -6, 3 then the roots of the equation 2(x2 + 3x − 18) = 0 are
Find the roots of the quadratic equation: x2 + 2x - 15 = 0?
Using the method of completion of squares find one of the roots of the equation 2x2 − 7x + 3 = 0. Also, find the equation obtained after completion of the square.
If the roots of a quadratic equation are 20 and -7, then find the equation?
Find the roots of the equation 5x2–6x–2=0 by the method of completing the square.
One root of the quadratic equation x2 - 12x + a = 0, is thrice the other. Find the value of a?
There is a natural number x. Write down the expression for the product of x and its next natural number.
What number should be added to x2 + 6x to make it a perfect square?
The equation x2 + 4x + c = 0 has real roots, then
Find the discriminant of the quadratic equation 3x2 – 5x + 2 = 0 and hence, find the nature of the roots.
Find the value of a/b + b/a, if a and b are the roots of the quadratic equation x2 + 8x + 4 = 0?
If the equation x2+2(k+2) x+9k=0 has equal roots, then values of k are __________.
Find the roots of the 3x2 – 5x + 2 = 0 quadratic equation, using the quadratic formula.