Test: Searching, Sorting & Hashing - 1 - Computer Science Engineering (CSE) MCQ
15 Questions MCQ Test - Test: Searching, Sorting & Hashing - 1
Which of the following is correct recurrence for worst case of Binary Search?
Consider the following C program that attempts to locate an element x in an array Y[] using binary search. The program is erroneous. (GATE CS 2008)
f(int Y[10], int x) {
int i, j, k;
i = 0; j = 9;
do {
k = (i + j) /2;
if( Y[k] < x) i = k; else j = k;
} while(Y[k] != x && i < j);
if(Y[k] == x) printf ("x is in the array ") ;
else printf (" x is not in the array ") ;
}
On which of the following contents of Y and x does the program fail?
f(int Y[10], int x) {
int i, j, k;
i = 0; j = 9;
do {
k = (i + j) /2;
if( Y[k] < x) i = k; else j = k;
} while(Y[k] != x && i < j);
if(Y[k] == x) printf ("x is in the array ") ;
else printf (" x is not in the array ") ;
}
Given a sorted array of integers, what can be the minimum worst case time complexity to find ceiling of a number x in given array? Ceiling of an element x is the smallest element present in array which is greater than or equal to x. Ceiling is not present if x is greater than the maximum element present in array. For example, if the given array is {12, 67, 90, 100, 300, 399} and x = 95, then output should be 100.
You are given a list of 5 integers and these integers are in the range from 1 to 6. There are no duplicates in list. One of the integers is missing in the list. Which of the following expression would give the missing number. ^ is bitwise XOR operator. ~ is bitwise NOT operator. Let elements of list can be accessed as list[0], list[1], list[2], list[3], list[4]
In the above question, the correction needed in the program to make it work properly is
Suppose we have a O(n) time algorithm that finds median of an unsorted array. Now consider a QuickSort implementation where we first find median using the above algorithm, then use median as pivot. What will be the worst case time complexity of this modified QuickSort.
What is recurrence for worst case of QuickSort and what is the time complexity in Worst case?
Which of the following sorting algorithms in its typical implementation gives best performance when applied on an array which is sorted or almost sorted (maximum 1 or two elements are misplaced).
Consider a situation where swap operation is very costly. Which of the following sorting algorithms should be preferred so that the number of swap operations are minimized in general?
Given an unsorted array. The array has this property that every element in array is at most k distance from its position in sorted array where k is a positive integer smaller than size of array. Which sorting algorithm can be easily modified for sorting this array and what is the obtainable time complexity?
How many different insertion sequences of the key values using the hash function h(k) = k mod 10 and linear probing will result in the hash table shown below?
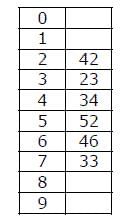
A hash table of length 10 uses open addressing with hash function h(k)=k mod 10, and linear probing. After inserting 6 values into an empty hash table, the table is as shown below.
Which one of the following choices gives a possible order in which the key values could have been inserted in the table?
The keys 12, 18, 13, 2, 3, 23, 5 and 15 are inserted into an initially empty hash table of length 10 using open addressing with hash function h(k) = k mod 10 and linear probing. What is the resultant hash table?
Given the following input (4322, 1334, 1471, 9679, 1989, 6171, 6173, 4199) and the hash function x mod 10, which of the following statements are true? i. 9679, 1989, 4199 hash to the same value ii. 1471, 6171 hash to the same value iii. All elements hash to the same value iv. Each element hashes to a different value
Which of the following statement(s) is TRUE?
- A hash function takes a message of arbitrary length and generates a fixed length code.
- A hash function takes a message of fixed length and generates a code of variable length.
- A hash function may give the same hash value for distinct messages.



















