Test: Graph Based Algorithms- 1 - Computer Science Engineering (CSE) MCQ
15 Questions MCQ Test - Test: Graph Based Algorithms- 1
Which of the following is an advantage of adjacency list representation over adjacency matrix representation of a graph?
What are the appropriate data structures for following algorithms?
1) Breadth First Search
2) Depth First Search
3) Prim's Minimum Spanning Tree
4) Kruskal' Minimum Spanning Tree
1) Breadth First Search
2) Depth First Search
3) Prim's Minimum Spanning Tree
4) Kruskal' Minimum Spanning Tree
The degree sequence of a simple graph is the sequence of the degrees of the nodes in the graph in decreasing order. Which of the following sequences can not be the degree sequence of any graph?
I. 7, 6, 5, 4, 4, 3, 2, 1
II. 6, 6, 6, 6, 3, 3, 2, 2
III. 7, 6, 6, 4, 4, 3, 2, 2
IV. 8, 7, 7, 6, 4, 2, 1, 1
I. 7, 6, 5, 4, 4, 3, 2, 1
II. 6, 6, 6, 6, 3, 3, 2, 2
III. 7, 6, 6, 4, 4, 3, 2, 2
IV. 8, 7, 7, 6, 4, 2, 1, 1
The Breadth First Search algorithm has been implemented using the queue data structure. One possible order of visiting the nodes of the following graph is
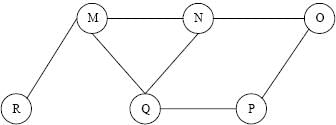
The most efficient algorithm for finding the number of connected components in an undirected graph on n vertices and m edges has time complexity. (A) θ(n) (B) θ(m) (C) θ(m + n) (D) θ(mn)
Let G be an undirected graph. Consider a depth-first traversal of G, and let T be the resulting depth-first search tree. Let u be a vertex in G and let v be the first new (unvisited) vertex visited after visiting u in the traversal. Which of the following statements is always true?
Consider an undirected unweighted graph G. Let a breadth-first traversal of G be done starting from a node r. Let d(r, u) and d(r, v) be the lengths of the shortest paths from r to u and v respectively, in G. lf u is visited before v during the breadth-first traversal, which of the following statements is correct?
How many undirected graphs (not necessarily connected) can be constructed out of a given set V= {V 1, V 2,…V n} of n vertices ?
Consider the following graph,
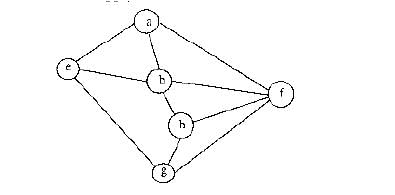
Among the following sequences:
(I) a b e g h f
(II) a b f e h g
(III) a b f h g e
(IV) a f g h b e
Which are depth first traversals of the above graph?
Which of the following statements is/are TRUE for an undirected graph? P: Number of odd degree vertices is even Q: Sum of degrees of all vertices is even
Make is a utility that automatically builds executable programs and libraries from source code by reading files called makefiles which specify how to derive the target program. Which of the following standard graph algorithms is used by Make.
Given two vertices in a graph s and t, which of the two traversals (BFS and DFS) can be used to find if there is path from s to t?
Consider an undirected random graph of eight vertices. The probability that there is an edge between a pair of vertices is 1/2. What is the expected number of unordered cycles of length three?
Is following statement true/false? A DFS of a directed graph always produces the same number of tree edges, i.e., independent of the order in which vertices are considered for DFS.
Given an undirected graph G with V vertices and E edges, the sum of the degrees of all vertices is















