Test: Linked List - Computer Science Engineering (CSE) MCQ
15 Questions MCQ Test - Test: Linked List
What does the following function do for a given Linked List with first node as head?
void fun1(struct node* head)
{
if(head == NULL)
return;
fun1(head->next);
printf("%d ", head->data);
}
{
if(head == NULL)
return;
fun1(head->next);
printf("%d ", head->data);
}
Which of the following sorting algorithms can be used to sort a random linked list with minimum time complexity?
The following function reverse() is supposed to reverse a singly linked list. There is one line missing at the end of the function.
/* Link list node */
struct node
{
int data;
struct node* next;
};
/* head_ref is a double pointer which points to head (or start) pointer
of linked list */
static void reverse(struct node** head_ref)
{
struct node* prev = NULL;
struct node* current = *head_ref;
struct node* next;
while (current != NULL)
{
next = current->next;
current->next = prev;
prev = current;
current = next;
}
/*ADD A STATEMENT HERE*/
}
What should be added in place of “/*ADD A STATEMENT HERE*/”, so that the function correctly reverses a linked list.
struct node
{
int data;
struct node* next;
};
/* head_ref is a double pointer which points to head (or start) pointer
of linked list */
static void reverse(struct node** head_ref)
{
struct node* prev = NULL;
struct node* current = *head_ref;
struct node* next;
while (current != NULL)
{
next = current->next;
current->next = prev;
prev = current;
current = next;
}
/*ADD A STATEMENT HERE*/
}
What should be added in place of “/*ADD A STATEMENT HERE*/”, so that the function correctly reverses a linked list.
What is the output of following function for start pointing to first node of following linked list?
1->2->3->4->5->6

The following C function takes a single-linked list of integers as a parameter and rearranges the elements of the list. The function is called with the list containing the integers 1, 2, 3, 4, 5, 6, 7 in the given order. What will be the contents of the list after the function completes execution?
struct node
{
int value;
struct node *next;
};
void rearrange(struct node *list)
{
struct node *p, * q;
int temp;
if ((!list) || !list->next)
return;
p = list;
q = list->next;
while(q)
{
temp = p->value;
p->value = q->value;
q->value = temp;
p = q->next;
q = p?p->next:0;
}
}
Suppose each set is represented as a linked list with elements in arbitrary order. Which of the operations among union, intersection, membership, cardinality will be the slowest?
Consider the function f defined below.
struct item
{
int data;
struct item * next;
};
int f(struct item *p)
{
return (
(p == NULL) ||
(p->next == NULL) ||
(( P->data <= p->next->data) && f(p->next))
);
}
For a given linked list p, the function f returns 1 if and only if
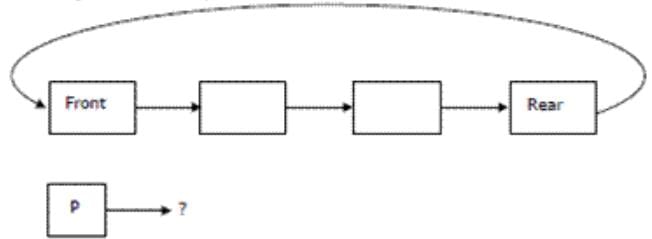
A circularly linked list is used to represent a Queue. A single variable p is used to access the Queue. To which node should p point such that both the operations enQueue and deQueue can be performed in constant time?
Given pointer to a node X in a singly linked list. Only one pointer is given, pointer to head node is not given, can we delete the node X from given linked list?
You are given pointers to first and last nodes of a singly linked list, which of the following operations are dependent on the length of the linked list?
Let P be a singly linked list. Let Q be the pointer to an intermediate node x in the list. What is the worst-case time complexity of the best known algorithm to delete the node x from the list?
N items are stored in a sorted doubly linked list. For a delete operation, a pointer is provided to the record to be deleted. For a decrease-key operation, a pointer is provided to the record on which the operation is to be performed. An algorithm performs the following operations on the list in this order:
Θ(N) delete, O(log N) insert, O(log N) find, and Θ(N) decrease-key
What is the time complexity of all these operations put together
The concatenation of two lists is to be performed in O(1) time. Which of the following implementations of a list should be used?
Consider the following statements:
i. First-in-first out types of computations are efficiently supported by STACKS.
ii. Implementing LISTS on linked lists is more efficient than implementing LISTS on an array for almost all the basic LIST operations.
iii. Implementing QUEUES on a circular array is more efficient than implementing QUEUES on a linear array with two indices.
iv. Last-in-first-out type of computations are efficiently supported by QUEUES.
Which of the following is correct?
A queue is implemented using a non-circular singly linked list. The queue has a head pointer and a tail pointer, as shown in the figure. Let n denote the number of nodes in the queue. Let ‘enqueue’ be implemented by inserting a new node at the head, and ‘dequeue’ be implemented by deletion of a node from the tail.

Which one of the following is the time complexity of the most time-efficient implementation of ‘enqueue’ and ‘dequeue, respectively, for this data structure?














