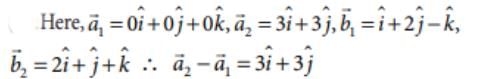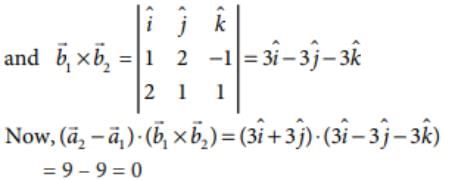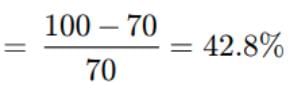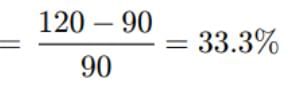UGEE REAP Mock Test- 1 - JEE MCQ
30 Questions MCQ Test - UGEE REAP Mock Test- 1
There is a 30% chance that it rains on any particular day. What is the probability that there is at least one rainy day within a period of 3 days?
Numbers are selected at random, one at a time, from the two-digit numbers 00,01,02,….99 with replacement. An event E occurs if and only if the product of the two digits of a selected number is 18. If four numbers are selected, find probability that the event E occurs at least 3 times.
A train going from Cambridge to London stops at 9 intermediate stations. Six persons enter the train during the journey with 6 different tickets of the same class. How many different sets of tickets would they have, given the correct number of journeys to be considered is from all station pairs?
Five balls of different colors are to be placed in three boxes of different sizes. Each box can hold all five balls. In how many different ways can we place the balls so that no box remains empty? (Note: Balls can get replaced.)
The harmonic mean of the roots of the equation (5 + √2)x2 - (4 + √5)x + 8 + 2√5 = 0 is
The tank at a water supply station is filled with water by several pumps. At first, two pumps of the same capacity are turned on; 3 hours later, three more pumps (all the same) of a different capacity are set into operation. After 2 hours, the additional pumps were set into operation; the tank was almost filled to its capacity (20 m³ were still lacking); in another hour the tank was full. One of the three additional pumps could have filled the tank in 60 hours.
How much water does one of the first two pumps fill in an hour?
In a transformer the number of primary turns is four times that of the secondary turns. Its primary is connected to an a.c. source of voltage V. Then
A transformer is used to light 100 W-110 V lamp from 220 V mains. If the main current is 0.5 A, the
efficiency of the transformer is
The direction ratios of line along which motorcycle B is running, are
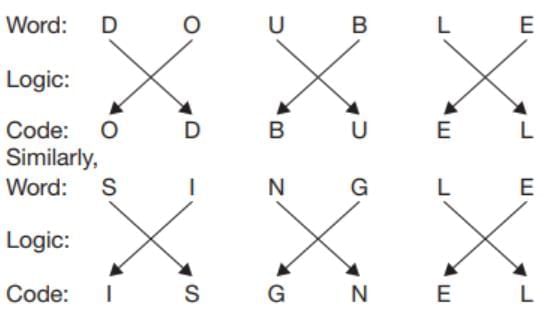
In a certain code language, if the word DOUBLE is coded as ODBUEL, then how is the word SINGLE coded in that language?
In a certain code language, if the word SUMMER is coded as Ωθ##17, and the word MOTION is coded as #$%2$6, then how can the word 'SECTOR' be coded in that language?
In a certain code language, if ADC is coded as 143 and BED is coded as 254 then how is DFG coded in that language?
Two circles APQC and PBDQ intersect each other at the points P and Q and APB and CQD are two parallel straight lines. Then only one of the following statements is always true. Which one is it?
If A + B means A is the mother of B; A - B means A is the brother B; A% B means A is the father of B and A × B means A is the sister of B, which of the following shows that P is the maternal uncle of Q?
Some people visit the theatre. The Venn diagram shows the number of people who bought ice cream and
drinks in the interval.
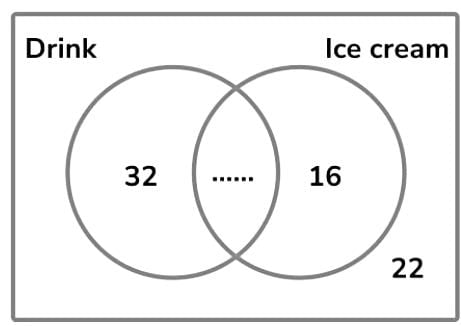
Ice cream is sold for €3 and drinks are sold for €2. A total of €262 is spent. How many people bought both a drink and an ice cream?
Which of the following, if true, most weakens the conclusion that the wellness program directly improves employee productivity?
Out of those employees knowing shorthand only, how many are graduates?
Alexander turned his attention toward India, since he had conquered Persia. Which one of the statements below is logically valid and can be inferred from the above sentence?
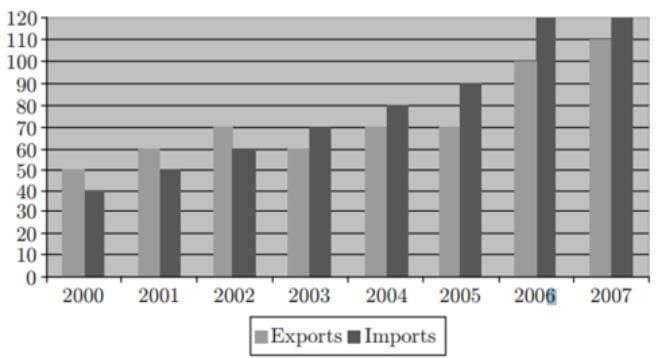
The exports and imports (in crores of Rs) of a country from the year 2000 to 2007 are given in the following bar chart. In which year is the combined percentage increase in imports and exports the highest?


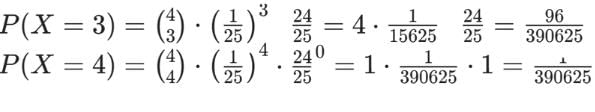
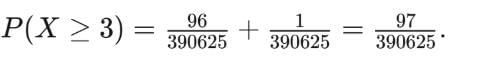

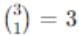 ways. The remaining 5 balls are placed in the 2 remaining boxes:
ways. The remaining 5 balls are placed in the 2 remaining boxes: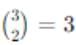 ways. The remaining 5 balls are placed in the 1 remaining box.
ways. The remaining 5 balls are placed in the 1 remaining box.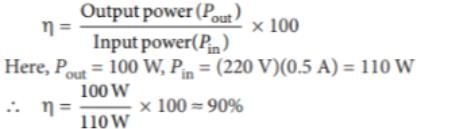
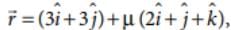 = which is parallel to the vector
= which is parallel to the vector