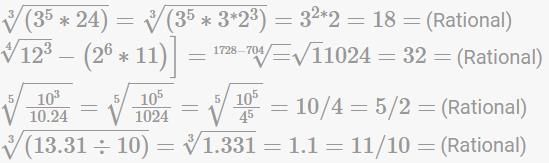All Courses
Get the App Signup / Login
Sign in Open App
Civil Engineering (CE) Exam  >  Civil Engineering (CE) Tests  >  RRB JE CE (CBT I) Mock Test- 2 - Civil Engineering (CE) MCQ

RRB JE CE (CBT I) Mock Test- 2 - Civil Engineering (CE) MCQ


Test Description

30 Questions MCQ Test - RRB JE CE (CBT I) Mock Test- 2

RRB JE CE (CBT I) Mock Test- 2 for Civil Engineering (CE) 2024 is part of Civil Engineering (CE) preparation. The RRB JE CE (CBT I) Mock Test- 2 questions and answers have been prepared according to the Civil Engineering (CE) exam syllabus.The RRB JE CE (CBT I) Mock Test- 2 MCQs are made for Civil Engineering (CE) 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for RRB JE CE (CBT I) Mock Test- 2 below.
Solutions of RRB JE CE (CBT I) Mock Test- 2 questions in English are available as part of our course for Civil Engineering (CE) & RRB JE CE (CBT I) Mock Test- 2 solutions in Hindi for Civil Engineering (CE) course. Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free. Attempt RRB JE CE (CBT I) Mock Test- 2 | 100 questions in 90 minutes | Mock test for Civil Engineering (CE) preparation | Free important questions MCQ to study for Civil Engineering (CE) Exam | Download free PDF with solutions
RRB JE CE (CBT I) Mock Test- 2 - Question 1
Save

In a school, 1000 chocolates were distributed in such a way that each student gets chocolates equal to 10% of the total students. Find the number of chocolates that each student gets

Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 1
Let the number of students = s

10 x s x s/100 = 1000

s2 = 10,000 s = 100

Each student got 10 x 100/100

=> 10 chocolates

RRB JE CE (CBT I) Mock Test- 2 - Question 2
Save

If the cost price of 12 pen is same as the selling price of 15 pen. What is the percentage of gain or loss?

Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 2
CP of 12 pen = SP of 15 pen CP x 12 = SP x 15

=> CP/SP - 5 / 4…(1)

From equation (1) we can see that CP >SP, therefore there will be loss. Let the CP = 5 and SP = 4 Then Loss = 1

Loss% = loss/CP x 100

= 1/5 x 100

= 20% loss

1 Crore+ students have signed up on EduRev. Have you? Download the App
RRB JE CE (CBT I) Mock Test- 2 - Question 3
Save

The following table represents marks obtained by four students in five subjects and maximum marks of each subject.

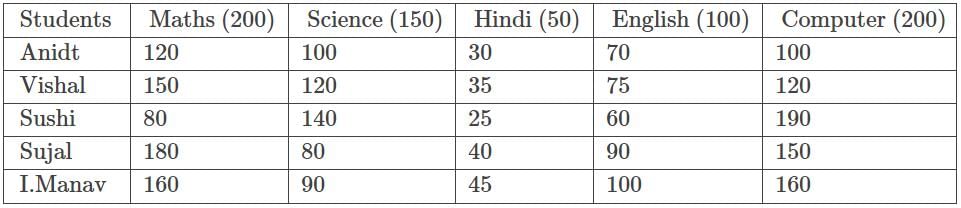
Q. Find the respective ratio of overall percentage of marks obtained by Ankil in all the five subjects and overall percentage of marks obtained by Sulal in all the five subjects.

Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 3
Total marks in all subjects = 200 + 150 + 50 + 100 + 200 = 700

Overall percentage of marks obtained by Ankit in all the five subjects

= (120 + 100 + 30 + 70 + 100)/700 x 100

= 420/700 x 100

= 60%

Overall percentage of marks obtained by Sujal in all the five subjects

= (180 + 80 + 40 + 90 + 150)/700 x 100

= 540/700 x 100

= 540/7%

Required ratio = 60 : 540/7

= 420 : 540

= 7 : 9

RRB JE CE (CBT I) Mock Test- 2 - Question 4
Save

Area of rhombus is (7 + 6.5√5) cm2 and length of its one diagonal is (3 + 2√5) cm, then what is the length of its second diagonal?
Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 4
Area of rhombus = (First diagonal x Second diagonal) / 2

2 x Area of rhombus = (First diagonal x Second diagonal)

Let its second diagonal = (a + b√5) cm

(14 + 13√5) = (3 + 2√5) x (a + b√5)

(14 + 13√5) = (3a + 3b√5 + 2a√5 + 10b)

After comparing-

(3a + 10b) = 14 ...... (1)

(2a + 3b) = 13 ....... (2)

From (1) and (2)-

a = 8 and b = -1

Length of second diagonal = (a + b√5) = (8 - √5) cm

RRB JE CE (CBT I) Mock Test- 2 - Question 5
Save

Solve the following expression: (∛42875 ÷ √49) + (152 - 21 x 10) - √625.
Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 5

= (∛42875 ÷ √49) + (152 - 21 x 10) - √625

= (35 ÷ 7) + (225 - 210) - 25

= 5 + 15 - 25

= -5

RRB JE CE (CBT I) Mock Test- 2 - Question 6
Save

A set of 7 pipes can fill 70% of a vessel in 7 minutes. Another set of 5 pipes can fill 2/5th of the vessel in 5 minutes. A third set of 10 pipes can empty 1/3rd of the tank in 10 minutes. How much time (in minutes) will it take to fill the entire tank if all the pipes are opened at the same time?
Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 6
7 pipes of first set can fill 7/10th of the vessel in 7 minutes.

Hence, 7 pipes of first set can fill 1/10th of the vessel in 1 min.

5 pipes of second set can fill 2/5th of the vessel in 5 minutes

Hence, 5 pipes of second set can fill 2/25th of the vessel in 1 min.

10 pipes of third set can empty 1/3rd of the vessel in 10 minutes.

Hence, 10 pipes of third set can empty 1/30th of the vessel in 1 min

So, if all the pipes are open in one minute 1/10 + 2/25 - 1/30 = 11/75th of the vessel is filled up.

Hence, to fill up the whole vessel, time required= 75/11 minutes.

RRB JE CE (CBT I) Mock Test- 2 - Question 7
Save

If an article is sold for a gain of 7% instead of selling it at a loss of 13%, a trader gets Rs.1080 more. What is the selling price of the article, when the article is sold at a profit of 25%?
Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 7
Let cost price of article be Rsx (13 + 7)% of x = 1080

20% of x = 1080

x = 5400

SP = 125% of 5400 = 6750

RRB JE CE (CBT I) Mock Test- 2 - Question 8
Save

There are total 10 students whose marks in an exam are 45, 65, 56, (P + 16), (2P + 3), 78, 24, (4P - 8), 44 and 48 respectively and mean marks of first 5 students is 49, then what is mean marks of last 5 students?
RRB JE CE (CBT I) Mock Test- 2 - Question 9
Save

Select the odd one out: (6 x 10-3), √[(52 + 11) x 10-6], (0.06 ÷ 102) and √0.000036.
Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 9
(6 x 10-3) = 0.006

√[(52 + 11) x 10-6] = 6 x 10-3 = 0.006

(0.06 ÷ 102) = 0.0006

√0.000036 = 0.006

RRB JE CE (CBT I) Mock Test- 2 - Question 10
Save

There is a fraction such that if we add 11/30 to it then it gets reverted. Further if we subtract 1 from numerator then the fraction becomes 2/3. What is the fraction?
Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 10
Let the fraction = m/n

According to the 1st condition; m/n + 11/30= n/m ...(1)

According to the 2nd condition; (m - 1)/n = ⅔

=> 3m - 3 = 2n

=> 3m - 2n = 3 ...(2)

By solving equation 1,

=> 30m2 + 11mn - 30n2 = 0

=> (6m - 5n)(5m + 6n) = 0

we get the value of m/n = 5/6, -6/5

applying condition(2), m/n = (5 - 1)/6 = 4/6 = 2/3

Hence the required fraction = m/n = 5/6

RRB JE CE (CBT I) Mock Test- 2 - Question 11
Save

How many among the following numbers are Irrational number: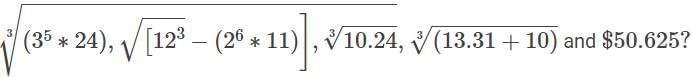

Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 11

RRB JE CE (CBT I) Mock Test- 2 - Question 12
Save

Ramesh and Suresh invested same amount of money in two banks for 2 years which offer interest at the same rate, but Ramesh invested in a bank which offers compound interest and Suresh invested in a bank which offers simple interest. After two years Ramesh got Rs. 525 as interest and Suresh got Rs. 500 as interest. What is the rate of interest offered by the banks?
Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 12
In case of simple interest we get the same amount of interest each year.

Hence amount of interest Suresh will get in first year = 500/2 = Rs. 250

If the same amount is invested and interest rate is same then in first year the interest obtained is same whether it is simple interest or compound interest.

Hence compound interest obtained in 1st year = Rs. 250

Therefore amount of interest obtained in the 2nd year = Rs. (525 - 250) = Rs. 275

Hence rate of interest = 100 x (275 - 250)/250 = 10%

RRB JE CE (CBT I) Mock Test- 2 - Question 13
Save

Line graph given below shows the total number of presence of employees in two different companies P and Q on five different working days from Monday to Friday.

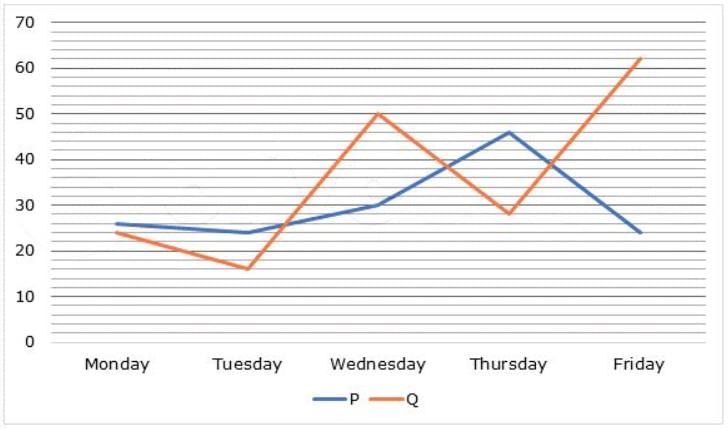
Q. What is the sum of the average number of presence of employees in company P and average number of presence of employees in company Q on all the five working days?
Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 13
Average number of presence of employees in company P on all the five working days = 26 + 24 + 30 + 46 + 24 = 150

Average = 150/5 = 30

Average number of presence of employees in company Q on all the five working days = 24 + 16 + 50 + 28 + 62 = 180

Average = 180/5 = 36

Required sum = 30 + 36 = 66

RRB JE CE (CBT I) Mock Test- 2 - Question 14
Save

If [(0.09)2 x (0.3)8 x (0.027) x 1012] / [312 x (0.3)x] = 1, then what is the value of x?
Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 14
[(0.09)2 x (0.3)8 x (0.027) x 1012] / [312 x (0.3)x] = 1

[(0.09)2 x (0.3)8 x (0.027) x 1012] = [312 x (0.3)x]

[(0.3)4 x (0.3)8 x (0.3)3] = [(0.3)12 x (0.3)x]

(0.3)15 / (0.3)12 = (0.3)x

(0.3)3 = (0.3)x

x = 3

RRB JE CE (CBT I) Mock Test- 2 - Question 15
Save

In one revolution, the object travels______ distance.
Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 15
In one revolution, the object travels 2πr distance. Revolution means a circular motion around an axis located outside the object. E.g., Rounding a curve in a car, merry go round, etc.
RRB JE CE (CBT I) Mock Test- 2 - Question 16
Save

Sita buys a parker pen at Rs. 100 and sell it to Geeta at Rs. 120. Geeta sells this pen to Radha at a price of Rs. 80. Radha sells it back to Sita at Rs. 90. Sita sells it to Roma at Rs. 150. What is Sita's profit/loss %?
Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 16
C.P. of pen for Sita = Rs 100

S.P. of pen for Sita = Rs 150 - 90 + 120 = 180

Profit % = [(180 - 100)/100] x 100 = 80%

RRB JE CE (CBT I) Mock Test- 2 - Question 17
Save

Mahesh is travelling at a distance of 1200 km in Japan by Bullet train. Due to some technical fault in the engine of the train, speed of the train was reduced by 100 km/hr thus overall time of his journey increased by 24 minutes. What was the normal speed of the bullet train?
Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 17
Let the normal speed of the bullet train is N km/hr and the corresponding time taken is A hours.

Hence; 1200/N = A .. (1)

According to the 2nd condition; 1200/(N - 100) = A + 2/5 .. (2)

Equation (2) - Equation (1); 1200/(N - 100) - 1200/N = 2/5

If we will try to solve this equation then it will become too lengthy. Hence such questions we should solve by using the options.

Out of the given options, option (c) satisfies above equation.

Hence; N = 600 km/hr

RRB JE CE (CBT I) Mock Test- 2 - Question 18
Save

If 4x - 1/3x = 9, then what is the value of (144x4 - 1)/(27x2 + 2x)?
Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 18
(12x2 - 1)/3x = 9

=> (12x2 - 1)/3x = 9

=> 12x2 - 1 = 27x ------- (i)

Now,

(144x4 - 1)/(27x2 + 2x)

= [(12x2 - 1)(12x2 + 1)]/[x(27x + 2)] ------- [(a2 - b2 = (a - b)(a + b)]

= [27x(27x -1 + 1 +1)]/[x(27x + 2)] ---- {Putting the value of equation (i)]

= [27x(27x + 2)]/[x(27x + 2)]

= 27

RRB JE CE (CBT I) Mock Test- 2 - Question 19
Save

What is the simplified value of (cos3 x/sin x) + (cos2 x.cot3 x)?
Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 19
cos3 x/sin x + cos2 x cot3 x

= (cos3 x/sin3 x) sin2 x + cos2 x cot3 x

= cot3 x sin2 x + cos2 x cot3 x

= cot3 x (sin2 x + cos2 x)

= cot3 x

RRB JE CE (CBT I) Mock Test- 2 - Question 20
Save

If 25% of (A + B) is 30% of (A - B), then B is what percent of A?
Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 20
=> 25/100(A + B) = 30/100(A - B)

=> 5A + 5B = 6A - 6B => A = 11B

=> Let p% of B is equal to A

=> p/100 x B = A

=> But B = 11A

RRB JE CE (CBT I) Mock Test- 2 - Question 21
Save

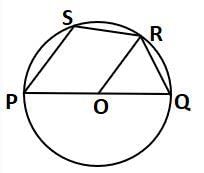
What is the ∠SRO if O is the centre of circle, ∠SPO = 550 and ∠POR = 1150
Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 21
In quadrilateral PQRS, ∠SRQ = 180∘ − ∠SPO = 180∘ − 55∘ = 125∘

[Sum of opposite angle of a cyclic quadrilateral is 1800.]

∠ROQ = 180∘ − ∠POR = 1800 − 115∘ = 65∘

In △QOR, ∠OQR = ∠ORQ [Angles opposite or same side] ∠ROQ + ∠OQR + ∠ORQ = 180∘

650 + ∠ORQ + ∠ORQ = 180∘

∠ORQ = (1800 − 65∘)/2 = 57.5∘

RRB JE CE (CBT I) Mock Test- 2 - Question 22
Save

A number 135 is split into three parts in such a way that all the three parts are in increasing Arithmetic Progression. The Product of the two largest parts is 2160, then what is the ratio of the smallest part to the highest part?
Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 22
Let the three numbers are: (a - d), a, (a + d) respectively.

According to questions:

a(a + d) = 2160 ...... (1)

(a - d) + a + (a + d) = 135

a = 45

From equation (1)

45(45 + d) = 2160

(45 + d) = 48

d = 3

Required ratio = (a - d) : (a + d) = 42 : 48 = 7 : 8

RRB JE CE (CBT I) Mock Test- 2 - Question 23
Save

Simplify the value of 3[{1/(√9 - √8)} - {1/(√9 + √8)}] + (2 - 3√2)2.
Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 23
= 3[{1/(√9 - √8)} - {1/(√9 + √8)}] + (2 - 3√2)2

= 3[{(√9 + √8) - (√9 - √8)}/(√9 - √8)(√9 + √8)] + (2 - 3√2)2

= 3[2√8] + (2 - 3√2)2

= 6√8 + (4 + 18 - 12√2)

= 12√2 + (22 - 12√2)

= 22

RRB JE CE (CBT I) Mock Test- 2 - Question 24
Save

There are 7 students in a class whose weights are: 54 kg, 45 kg, 48 kg, A kg, 42 kg, 50 kg and 55 kg. If the mean of their weights is 49 kg, then what is the median of their weights?
Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 24
Mean of their weights = (54 + 45 + 48 + A + 42 + 50 + 55)/7 = 49

294 + A = 343

A = 49 kg

Arrange the weights in ascending order = 42, 45, 48, 49, 50, 54, 55

Median of their weights = 4th term in series = 49 kg

RRB JE CE (CBT I) Mock Test- 2 - Question 25
Save

The LCM of two numbers is 2376, and their HCF is 22. Find their difference, if the sum of numbers is 682.
Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 25
Let the number be 22x and 22y

22x + 22y = 682

x + y = 31 → (1)

22x x 22y = 2376 x 22

xy = 108 → (2)

Solving (1) and (2), we get

x = 27 and y = 4

Difference = 22x - 22y

= 22(27 - 4)

= 22 x 23

= 506

RRB JE CE (CBT I) Mock Test- 2 - Question 26
Save

60 liters of first mixture of milk and water is mixed with another 40 liters mixture of milk and water. After mixing the mixture, the mixture is sold at the cost of pure milk, then what is the percent profit gained if the ratio of milk to water in the first and second mixture is 7: 5 and 3: 5, respectively? Given below are the steps involved. Arrange them in sequential order.

(A) Amount of milk and water in first mixture is 60 x (7/12) = 35 liters and 60 x (5/12) = 25 liters respectively.

(B) Total amount of milk and water is final mixture is (35 + 15) = 50 liters and (25 + 25) = 50 liters respectively.

(C) Percent profit earned = [(100 - 50)/50] x 100 = 100%

(D) Amount of milk and water in second mixture is 40 x (3/8) = 15 liters and 40 x (5/8) = 25 litres respectively.

(E) Cost price of final mixture = 50 x 1 = 50 and selling price of final mixture = 100 x 1 = 100
Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 26
The correct arrangement is:

(A) Amount of milk and water in first mixture is 60 x (7/12) = 35 litres and 60 x (5/12) = 25 liters respectively.

(D) Amount of milk and water in second mixture is 40 x (3/8) = 15 liters and 40 x (5/8) = 25 liters respectively.

(B) Total amount of milk and water is final mixture is (35 + 15) = 50 litres and (25 + 25) = 50 liters respectively.

(E) Cost price of final mixture = 50 x 1 = 50 and selling price of final mixture = 100 x 1 = 100

(C) Per cent profit earned = [(100 - 50)/50] x 100 = 100%

RRB JE CE (CBT I) Mock Test- 2 - Question 27
Save

If cosec θ = x + 1/4x, then the value of cosec θ + cot θ is:
Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 27

Given that cosec θ = x + 1/(4x). We need to find the value of cosec θ + cot θ. Let's denote cosec θ + cot θ as k. So, k = cosec θ + cot θ Using the identity: cosec²θ - cot²θ = 1 We can express cosec θ - cot θ as: cosec θ - cot θ = 1/k Now, add the two expressions: (cosec θ + cot θ) + (cosec θ - cot θ) = k + 1/k This simplifies to: 2 cosec θ = k + 1/k Substitute the given value of cosec θ: 2(x + 1/(4x)) = k + 1/k 2x + 1/(2x) = k + 1/k To solve for k, assume k = 2x. Substitute k = 2x into the equation: 2x + 1/(2x) = 2x + 1/(2x) Both sides of the equation are equal, confirming that k = 2x is the correct value. Therefore, the value of cosec θ + cot θ is 2x.

RRB JE CE (CBT I) Mock Test- 2 - Question 28
Save

At present, the sum of ages of R and K is 63 years. The ratio of their ages after 7 years will be 7: 4 , what is the present age of R?
Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 28
Let the present age of R is x

⇒ present age of K is 63 - x

7 years later

R's age = x + 7

K's age = 63 - x + 7= 70 - x

⇒ (x + 7) / (70 - x) = 7 / 4

⇒ 4x + 28= 490 - 7x

⇒ 11x = 462

⇒ x = 42 years

therefore present age of R = 42 years

RRB JE CE (CBT I) Mock Test- 2 - Question 29
Save

If 5 girls can embroider a dress in 9 days, then the number of days taken by 3 girls will be _____.
Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 29
Days taken by 5 girls to embroider a dress = 9 days

Days taken by 1 girl to embroider a dress = 9 x 5 days

Days taken by 3 girls to embroider a dress = 9 × 5/3 days = 15 days

RRB JE CE (CBT I) Mock Test- 2 - Question 30
Save

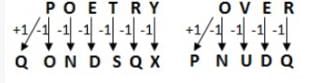
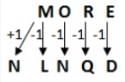
In a certain code language, ‘POETRY’ is written as ‘QONDSQX’ and ‘OVER’ is written as ‘PNUDQ.’ How is ‘MORE’ written in that code language?
Detailed Solution for RRB JE CE (CBT I) Mock Test- 2 - Question 30
AS

SIMILARLY

View more questions
Information about RRB JE CE (CBT I) Mock Test- 2 Page
In this test you can find the Exam questions for RRB JE CE (CBT I) Mock Test- 2 solved & explained in the simplest way possible. Besides giving Questions and answers for RRB JE CE (CBT I) Mock Test- 2, EduRev gives you an ample number of Online tests for practice

Top Courses for Civil Engineering (CE)

Download as PDF

Top Courses for Civil Engineering (CE)

Important Questions for RRB JE CE (CBT I) Mock Test- 2

Find all the important questions for RRB JE CE (CBT I) Mock Test- 2 at EduRev.Get fully prepared for RRB JE CE (CBT I) Mock Test- 2 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the RRB JE CE (CBT I) Mock Test- 2 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of RRB JE CE (CBT I) Mock Test- 2 resources.

RRB JE CE (CBT I) Mock Test- 2 MCQs with Answers

Prepare for the RRB JE CE (CBT I) Mock Test- 2 within the Civil Engineering (CE) exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for RRB JE CE (CBT I) Mock Test- 2

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace RRB JE CE (CBT I) Mock Test- 2 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup