Test: Inverse Trigonometric Functions- Case Based Type Questions - Commerce MCQ
15 Questions MCQ Test - Test: Inverse Trigonometric Functions- Case Based Type Questions
Direction: Read the following text and answer the following questions on the basis of the same:
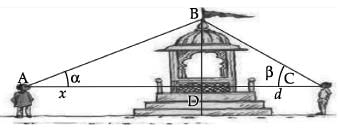
Two men on either side of a temple of 30 metres high observe its top at the angles of elevation α and β respectively. (as shown in the figure above). The distance between the two men is 40√3 metres and the distance between the first person A and the temple is 30√3 meters.
∠CAB = α =

Direction: Read the following text and answer the following questions on the basis of the same:
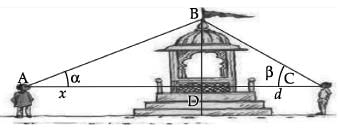
Two men on either side of a temple of 30 metres high observe its top at the angles of elevation α and β respectively. (as shown in the figure above). The distance between the two men is 40√3 metres and the distance between the first person A and the temple is 30√3 meters.
Domain and Range of cos−1 x =

Direction: Read the following text and answer the following questions on the basis of the same:
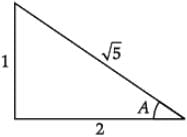
In the school project Sheetal was asked to construct a triangle and name it as ABC. Two angles A and B were given to be equal to tan-1(½) and tan-1(⅓) respectively.
The value of sin A is _______.

Direction: Read the following text and answer the following questions on the basis of the same:
In the school project Sheetal was asked to construct a triangle and name it as ABC. Two angles A and B were given to be equal to tan-1(½) and tan-1(⅓) respectively.
The third angle, ∠C = _______.
Direction: Read the following text and answer the following questions on the basis of the same:
The value of an inverse trigonometric functions which lies in the range of Principal branch is called the principal value of that inverse trigonometric functions.
Principal value of sin–1 (½) is
Direction: Read the following text and answer the following questions on the basis of the same:
The value of an inverse trigonometric functions which lies in the range of Principal branch is called the principal value of that inverse trigonometric functions.
Principal value of 2cos–1 (1) + 5tan–1 (1) is:
Direction: Read the following text and answer the following questions on the basis of the same:
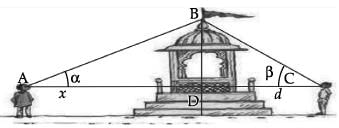
Two men on either side of a temple of 30 metres high observe its top at the angles of elevation α and β respectively. (as shown in the figure above). The distance between the two men is 40√3 metres and the distance between the first person A and the temple is 30√3 meters.
∠CAB = α =
Direction: Read the following text and answer the following questions on the basis of the same:
In the school project Sheetal was asked to construct a triangle and name it as ABC. Two angles A and B were given to be equal to tan-1(½) and tan-1(⅓) respectively.
cos(A + B + C) = _______.
Direction: Read the following text and answer the following questions on the basis of the same:
The value of an inverse trigonometric functions which lies in the range of Principal branch is called the principal value of that inverse trigonometric functions.
Principal value of tan–1 (1)
Direction: Read the following text and answer the following questions on the basis of the same:
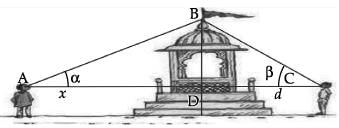
Two men on either side of a temple of 30 metres high observe its top at the angles of elevation α and β respectively. (as shown in the figure above). The distance between the two men is 40√3 metres and the distance between the first person A and the temple is 30√3 meters.
∠BCA = β =
Direction: Read the following text and answer the following questions on the basis of the same:
In the school project Sheetal was asked to construct a triangle and name it as ABC. Two angles A and B were given to be equal to tan-1(½) and tan-1(⅓) respectively.
If B = cos–1 x, then x = _______.
Direction: Read the following text and answer the following questions on the basis of the same:
The value of an inverse trigonometric functions which lies in the range of Principal branch is called the principal value of that inverse trigonometric functions.
Principal value of cot-1(√3) is :
Direction: Read the following text and answer the following questions on the basis of the same:
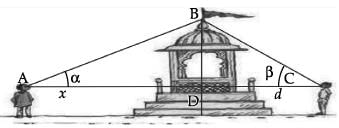
Two men on either side of a temple of 30 metres high observe its top at the angles of elevation α and β respectively. (as shown in the figure above). The distance between the two men is 40√3 metres and the distance between the first person A and the temple is 30√3 meters.
∠ABC =
Direction: Read the following text and answer the following questions on the basis of the same:
In the school project Sheetal was asked to construct a triangle and name it as ABC. Two angles A and B were given to be equal to tan-1(½) and tan-1(⅓) respectively.
If A = sin–1x; then the value of x is:
Direction: Read the following text and answer the following questions on the basis of the same:
The value of an inverse trigonometric functions which lies in the range of Principal branch is called the principal value of that inverse trigonometric functions.
Principal value of sin -1(1) + sin-1(1/√2) is