Test: Understanding Quadrilaterals- 2 - Class 8 MCQ
20 Questions MCQ Test - Test: Understanding Quadrilaterals- 2
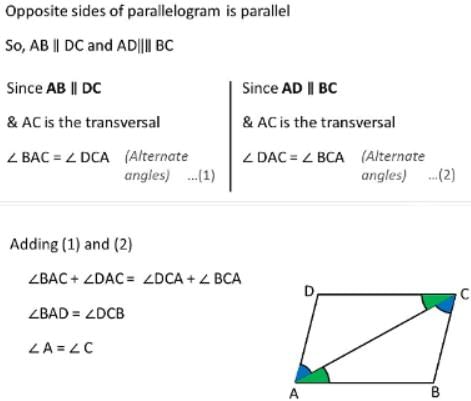
Which of the following is true for the adjacent angles of a parallelogram?
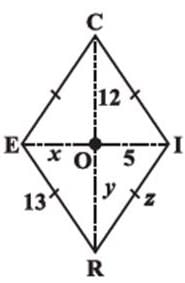
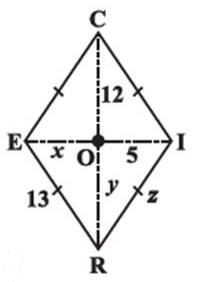
Which of the following quadilaterals has two pairs of adjacent sides equal and diagonals intersecting at right angles?
State the name of a regular polygon of 6 sides.
Find the measure of each exterior angle of a regular polygon of 9 sides.
The sides of a pentagon are produced in order. Which of the following is the sum of its exterior angles?
ABCD is a quadrilateral. If AC and BD bisect each other, what is ABCD?
A _______ is both ‘equiangular’ and ‘equilateral’.
A _________ has all the properties of a parallelogram and also that of a kite.
Find the value of the unknown y. If ABCD is a parallelogram ?
A simple closed curve made up of only line segments is called a ________.
A _________ is a quadrilateral whose opposite sides are parallel.
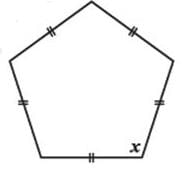
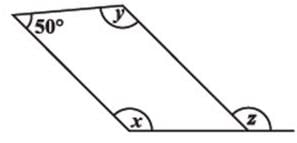
Find the angle measure x in the following figure: