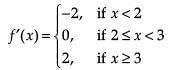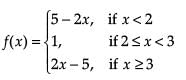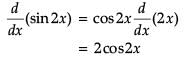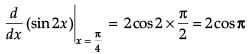Test: Continuity and Differentiability- Case Based Type Questions - Commerce MCQ
10 Questions MCQ Test - Test: Continuity and Differentiability- Case Based Type Questions
Direction: Read the following text and answer the following questions on the basis of the same:
A potter made a mud vessel, where the shape of the pot is based on f(x) = |x – 3| + |x – 2|, where f(x) represents the height of the pot.
If the potter is trying to make a pot using the function f(x) = [x], will he get a pot or not? Why?
Direction: Read the following text and answer the following questions on the basis of the same:
A potter made a mud vessel, where the shape of the pot is based on f(x) = |x – 3| + |x – 2|, where f(x) represents the height of the pot.
Will the slope vary with x value?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Direction: Read the following text and answer the following questions on the basis of the same:
A potter made a mud vessel, where the shape of the pot is based on f(x) = |x – 3| + |x – 2|, where f(x) represents the height of the pot.
When the value of x lies between (2, 3) then the function is
Direction: Read the following text and answer the following questions on the basis of the same:
A potter made a mud vessel, where the shape of the pot is based on f(x) = |x – 3| + |x – 2|, where f(x) represents the height of the pot.
When x > 4 what will be the height in terms of x?
Direction: Read the following text and answer the following questions on the basis of the same:
A potter made a mud vessel, where the shape of the pot is based on f(x) = |x – 3| + |x – 2|, where f(x) represents the height of the pot.
What is dy/dx at x = 3
Direction: Read the following text and answer the following questions on the basis of the same:
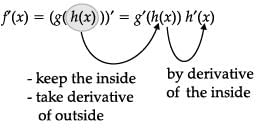
Ms. Remka of city school is teaching chain rule to her students with the help of a flow-chart
The chain rule says that if h and g are functions and f(x) = g(h(x)), then
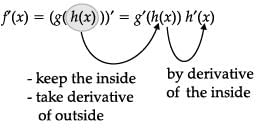
Let f(x) = sin x and g(x) = x3
d/dx (sin2x) at x = π/2 is ____.
Direction: Read the following text and answer the following questions on the basis of the same:
Ms. Remka of city school is teaching chain rule to her students with the help of a flow-chart
The chain rule says that if h and g are functions and f(x) = g(h(x)), then
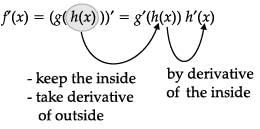
Let f(x) = sin x and g(x) = x3
gof(x) = _______.
Direction: Read the following text and answer the following questions on the basis of the same:
Ms. Remka of city school is teaching chain rule to her students with the help of a flow-chart
The chain rule says that if h and g are functions and f(x) = g(h(x)), then
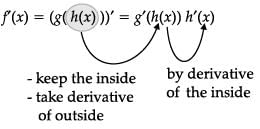
Let f(x) = sin x and g(x) = x3
d/dx sin x3 _______.
Direction: Read the following text and answer the following questions on the basis of the same:
Ms. Remka of city school is teaching chain rule to her students with the help of a flow-chart
The chain rule says that if h and g are functions and f(x) = g(h(x)), then
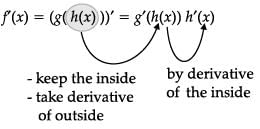
Let f(x) = sin x and g(x) = x3
fog(x) = _______.
Direction: Read the following text and answer the following questions on the basis of the same:
Ms. Remka of city school is teaching chain rule to her students with the help of a flow-chart
The chain rule says that if h and g are functions and f(x) = g(h(x)), then
Let f(x) = sin x and g(x) = x3
d/dx (sin3 x) = _______.
Top Courses for Commerce
Important Questions for Continuity and Differentiability- Case Based Type Questions
Continuity and Differentiability- Case Based Type Questions MCQs with Answers
Online Tests for Continuity and Differentiability- Case Based Type Questions
|
© EduRev
|
Education Revolution
|
Follow Us
|
