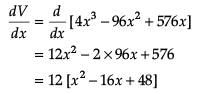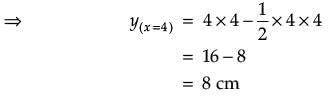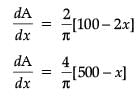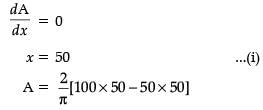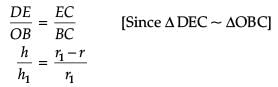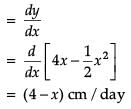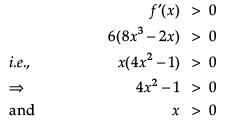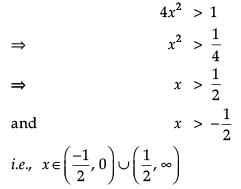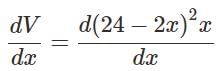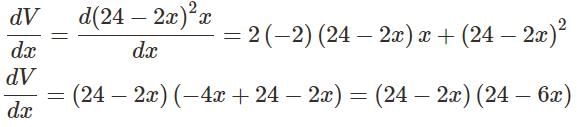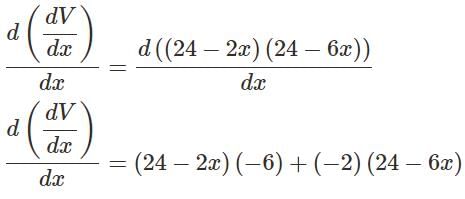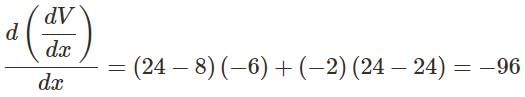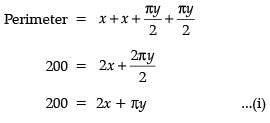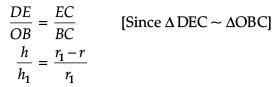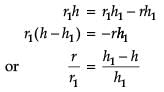All Courses
Get the App Signup / Login
Sign in Open App
Commerce Exam  >  Commerce Tests  >  Test: Application of Derivatives- Case Based Type Questions- 1 - Commerce MCQ

Test: Application of Derivatives- Case Based Type Questions- 1 - Commerce MCQ


Test Description

15 Questions MCQ Test - Test: Application of Derivatives- Case Based Type Questions- 1

Test: Application of Derivatives- Case Based Type Questions- 1 for Commerce 2024 is part of Commerce preparation. The Test: Application of Derivatives- Case Based Type Questions- 1 questions and answers have been prepared according to the Commerce exam syllabus.The Test: Application of Derivatives- Case Based Type Questions- 1 MCQs are made for Commerce 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Application of Derivatives- Case Based Type Questions- 1 below.
Solutions of Test: Application of Derivatives- Case Based Type Questions- 1 questions in English are available as part of our course for Commerce & Test: Application of Derivatives- Case Based Type Questions- 1 solutions in Hindi for Commerce course. Download more important topics, notes, lectures and mock test series for Commerce Exam by signing up for free. Attempt Test: Application of Derivatives- Case Based Type Questions- 1 | 15 questions in 30 minutes | Mock test for Commerce preparation | Free important questions MCQ to study for Commerce Exam | Download free PDF with solutions
Test: Application of Derivatives- Case Based Type Questions- 1 - Question 1
Save

Read the following text and answer the following questions. On the basis of the same:

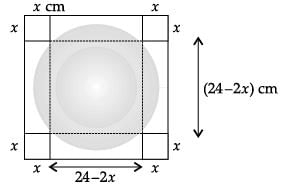
An open box is to be made out of a piece of cardboard measuring (24 cm × 24 cm) by cutting of equal squares from the corners and turning up the sides.

Find the value of dV/dx ?

Detailed Solution for Test: Application of Derivatives- Case Based Type Questions- 1 - Question 1

Test: Application of Derivatives- Case Based Type Questions- 1 - Question 2
Save

Read the following text and answer the following questions, on the basis of the same:

The Relation between the height of the plant (y in cm) with respect to exposure to sunlight is governed by the following equation y = 4x – 1/2x2. where x is the number of days exposed to sunlight.

What is the maximum height of the plant?

Detailed Solution for Test: Application of Derivatives- Case Based Type Questions- 1 - Question 2

We have, number of days for maximum height of plant = 4 days

∴ Maximum height of plant

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: Application of Derivatives- Case Based Type Questions- 1 - Question 3
Save

Read the following text and answer the following questions on the basis of the same: The shape of a toy is given as f(x) = 6(2x4 – x2). To make the toy beautiful 2 sticks which are perpendicular to each other were placed at a point (2, 3), above the toy.

Find the second order derivative of the function at x = 5.

Detailed Solution for Test: Application of Derivatives- Case Based Type Questions- 1 - Question 3
f(x) = 6(2x4 - x2)

f’(x) = 6[8x3 - 2x]

f”(x) = 6[24x2 - 2]

f”(5) = 6[24 x 25 - 2]

= 6[600 - 2]

= 3588

Test: Application of Derivatives- Case Based Type Questions- 1 - Question 4
Save

Read the following text and answer the following questions on the basis of the same:

P(x) = –5x2 + 125x + 37500 is the total profit function of a company, where x is the production of the company.

What will be the production when the profit is maximum?
Detailed Solution for Test: Application of Derivatives- Case Based Type Questions- 1 - Question 4

We, have

p(x) =-5x2 + 125x+ 37500

p’(x) = -10x + 125

For maximum profit

p’(x) = 0

-10x + 125 = 0

-10x = -125

x = 125/10

= 12.5

Test: Application of Derivatives- Case Based Type Questions- 1 - Question 5
Save

Read the following text and answer the following questions, on the basis of the same:

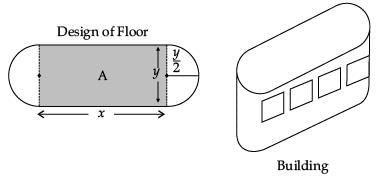
An architect designs a building for a multi-national company. The floor consists of a rectangular region with semicircular ends having a perimeter of 200 m as shown below:

The maximum value of area A is :
Detailed Solution for Test: Application of Derivatives- Case Based Type Questions- 1 - Question 5

For maxima,

Test: Application of Derivatives- Case Based Type Questions- 1 - Question 6
Save

Read the following text and answer the following questions on the basis of the same:

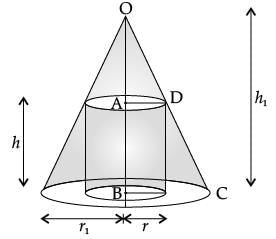
A right circular cylinder is inscribed in a cone.

S = Curved Surface Area of Cylinder.

r/r1 = ?
Detailed Solution for Test: Application of Derivatives- Case Based Type Questions- 1 - Question 6

In ?DEC and ? OBC

Test: Application of Derivatives- Case Based Type Questions- 1 - Question 7
Save

Read the following text and answer the following questions, on the basis of the same:

The Relation between the height of the plant (y in cm) with respect to exposure to sunlight is governed by the following equation y = 4x – 1/2x2. where x is the number of days exposed to sunlight.

The rate of growth of the plant with respect to sunlight is ______ .
Detailed Solution for Test: Application of Derivatives- Case Based Type Questions- 1 - Question 7

∴ rate of growth of the plant with respect to sunlight

Test: Application of Derivatives- Case Based Type Questions- 1 - Question 8
Save

Read the following text and answer the following questions on the basis of the same: The shape of a toy is given as f(x) = 6(2x4 – x2). To make the toy beautiful 2 sticks which are perpendicular to each other were placed at a point (2, 3), above the toy.

At which of the following intervals will f(x) be increasing?
Detailed Solution for Test: Application of Derivatives- Case Based Type Questions- 1 - Question 8

For increasing

Test: Application of Derivatives- Case Based Type Questions- 1 - Question 9
Save

Read the following text and answer the following questions. On the basis of the same:

An open box is to be made out of a piece of cardboard measuring (24 cm × 24 cm) by cutting of equal squares from the corners and turning up the sides.

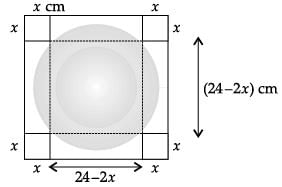
Find the value of x other than 12?
Detailed Solution for Test: Application of Derivatives- Case Based Type Questions- 1 - Question 9
The length x is cut from every corner of the paper so that we can fold it and it looks like an open box.

It means the height of the box is x cm.

Then the volume of the box will be (24 − 2x)2x.

On solving it further we get the volume V as:

V = (24 − 2x)2x

On differentiating the above volume with respect to x we get,

We will use here uv rule to differentiate the term.

When we differentiate uv that is (uv)’ we get (uv)’ = u’v + uv’.

On equating it to zero to get the value of x,

We got the value of x = 12, 4.

The value of x as 12 will be neglected because it will not be a box if we cut the length of 12cm from both the sides. So, the value of x is 4cm.

And the maximum volume of box will be ⇒ (24 − 2(4))2(4) = 1024cm3

We need to find the height when the volume is maximum. If we observe the figure we can clearly see that x is the height itself and it is 4cm.

If we want to check that the maximum volume will be at 4 or not we will double differentiate the volume at 4 and if it is negative it means this point is point of maxima so, we do,

On putting the value of x = 4 in the above equation we get,

Hence the value is negative so, point 4 is the point of maxima.

Test: Application of Derivatives- Case Based Type Questions- 1 - Question 10
Save

Read the following text and answer the following questions on the basis of the same:

P(x) = –5x2 + 125x + 37500 is the total profit function of a company, where x is the production of the company.

Check in which interval the profit is strictly increasing .
Detailed Solution for Test: Application of Derivatives- Case Based Type Questions- 1 - Question 10
Profit is strictly increasing where

P’(x) > 0

-10x + 125 >0

125 > 10x

10x < 125

X < 12.5

So, profit is strictly increasing for x ∈ (0, 12.5)

Test: Application of Derivatives- Case Based Type Questions- 1 - Question 11
Save

Read the following text and answer the following questions, on the basis of the same:

An architect designs a building for a multi-national company. The floor consists of a rectangular region with semicircular ends having a perimeter of 200 m as shown below:

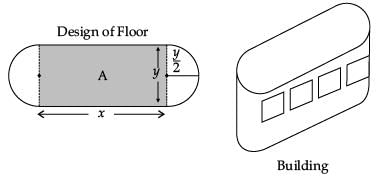
If x and y represents the length and breadth of the rectangular region, then the relation between the variables is :
Detailed Solution for Test: Application of Derivatives- Case Based Type Questions- 1 - Question 11

Test: Application of Derivatives- Case Based Type Questions- 1 - Question 12
Save

Read the following text and answer the following questions on the basis of the same:

A right circular cylinder is inscribed in a cone.

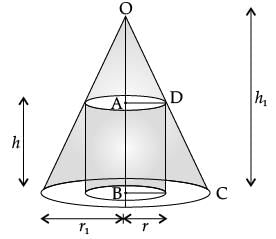
S = Curved Surface Area of Cylinder.

r/r1 = ?
Detailed Solution for Test: Application of Derivatives- Case Based Type Questions- 1 - Question 12

In ?DEC and ? OBC

Test: Application of Derivatives- Case Based Type Questions- 1 - Question 13
Save

Read the following text and answer the following questions on the basis of the same: The shape of a toy is given as f(x) = 6(2x4 – x2). To make the toy beautiful 2 sticks which are perpendicular to each other were placed at a point (2, 3), above the toy.

Which value from the following may be abscissa of critical point?
Detailed Solution for Test: Application of Derivatives- Case Based Type Questions- 1 - Question 13
Critical point is point where f’(x) = 0

Test: Application of Derivatives- Case Based Type Questions- 1 - Question 14
Save

Read the following text and answer the following questions on the basis of the same:

A right circular cylinder is inscribed in a cone.

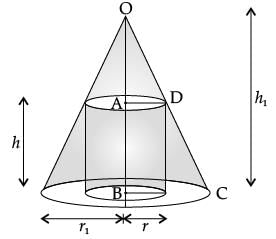
What is the value of dS/dh?
Detailed Solution for Test: Application of Derivatives- Case Based Type Questions- 1 - Question 14

Test: Application of Derivatives- Case Based Type Questions- 1 - Question 15
Save

Read the following text and answer the following questions. On the basis of the same:

An open box is to be made out of a piece of cardboard measuring (24 cm × 24 cm) by cutting of equal squares from the corners and turning up the sides.

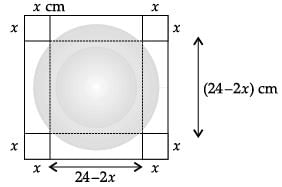
Volume is maximum at what height of that open box?
Detailed Solution for Test: Application of Derivatives- Case Based Type Questions- 1 - Question 15

For maximum value,

dV/dx = 0

i.e., 12(x2 - 16x + 48) = 0

X2 - 16 x + 48 = 0

x2 - 4x - 12x + 48 = 0

x(x - 4) - 12(x - 4) = 0

(x - 4)(x - 12) = 0

X = 4, 12

V(x = 4) = (24 - 2 x 4)(24 - 2 x 4) x 4

= 16 x 16 x 4

Information about Test: Application of Derivatives- Case Based Type Questions- 1 Page
In this test you can find the Exam questions for Test: Application of Derivatives- Case Based Type Questions- 1 solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Application of Derivatives- Case Based Type Questions- 1, EduRev gives you an ample number of Online tests for practice

Top Courses for Commerce

Download as PDF

Top Courses for Commerce

Important Questions for Application of Derivatives- Case Based Type Questions- 1

Find all the important questions for Application of Derivatives- Case Based Type Questions- 1 at EduRev.Get fully prepared for Application of Derivatives- Case Based Type Questions- 1 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Application of Derivatives- Case Based Type Questions- 1 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Application of Derivatives- Case Based Type Questions- 1 resources.

Application of Derivatives- Case Based Type Questions- 1 MCQs with Answers

Prepare for the Application of Derivatives- Case Based Type Questions- 1 within the Commerce exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Application of Derivatives- Case Based Type Questions- 1

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Application of Derivatives- Case Based Type Questions- 1 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup