CAT 2020 Slot 3: Past Year Question Paper - CAT MCQ
30 Questions MCQ Test - CAT 2020 Slot 3: Past Year Question Paper
The author is least likely to agree with the view that the increase in screen-time is fuelled by the fact that:
The author claims that Silicon Valley tech companies have tried to “confuse the public” by:
The statement “The richer you are, the more you spend to be off-screen” is supported by which other line from the passage?
Which of the following statements about the negative effects of screen time is the author least likely to endorse?
Which one of the following best captures the main argument of the last paragraph of the passage?
Which one of the following, if true, would be an accurate inference from the first sentence of the passage?
Which one of the following, if false, could be seen as supporting the author’s claims?
All of the following, if true, could be seen as supporting the arguments in the passage, EXCEPT:
According to the passage, the author is likely to be supportive of which one of the following programmes?
According to the passage, Said’s book, “Orientalism”:
From the passage, it can be inferred that scholars argue that Victorian women experienced self-development through their travels because:
American travel literature of the 1920s:
From the passage, we can infer that feminist scholars’ understanding of the experiences of Victorian women travellers is influenced by all of the following EXCEPT scholars':
From the passage, we can infer that travel writing is most similar to:
According to the author, the main reason why Bregman contrasts life in preagricultural societies with agricultural societies is to:
None of the following views is expressed in the passage EXCEPT that:
According to the passage, the “collapse of civilisations” is viewed by Bregman as:
The author has differing views from Bregman regarding:
The four sentences (labelled 1, 2, 3, 4) below, when properly sequenced would yield a coherent paragraph. Decide on the proper sequencing of the order of the sentences and key in the sequence of the four numbers as your answer:
1. Each one personified a different aspect of good fortune.
2. The others were versions of popular Buddhist gods, Hindu gods and Daoist gods.
3. Seven popular Japanese deities, the Shichi Fukujin, were considered to bring good luck and happiness.
4. Although they were included in the Shinto pantheon, only two of them, Daikoku and Ebisu, were indigenous Japanese gods.
Five jumbled up sentences, related to a topic, are given below. Four of them can be put together to form a coherent paragraph. Identify the odd one out and key in the number of the sentence as your answer:
The passage given below is followed by four alternate summaries. Choose the option that best captures the essence of the passage.
Brown et al. (2001) suggest that ‘metabolic theory may provide a conceptual foundation for much of ecology just as genetic theory provides a foundation for much of evolutionary biology’. One of the successes of genetic theory is the diversity of theoretical approaches and models that have been developed and applied. A Web of Science (v. 5.9. Thomson Reuters) search on genetic* + theor* + evol* identifies more than 12000 publications between 2005 and 2012. Considering only the 10 most-cited papers within this 12000 publication set, genetic theory can be seen to focus on genome dynamics, phylogenetic inference, game theory and the regulation of gene expression. There is no one fundamental genetic equation, but rather a wide array of genetic models, ranging from simple to complex, with differing inputs and outputs, and divergent areas of application, loosely connected to each other through the shared conceptual foundation of heritable variation.
The four sentences (labelled 1, 2, 3, 4) below, when properly sequenced would yield a coherent paragraph. Decide on the proper sequencing of the order of the sentences and key in the sequence of the four numbers as your answer:
1. It advocated a conservative approach to antitrust enforcement that espouses faith in efficient markets and voiced suspicion regarding the merits of judicial intervention to correct anticompetitive practices.
2. Many industries have consistently gained market share, the lion’s share – without any official concern; the most successful technology companies have grown into veritable titans, on the premise that they advance ‘public interest’.
3. That the new anticompetitive risks posed by tech giants like Google, Facebook, and Amazon, necessitate new legal solutions could be attributed to the dearth of enforcement actions against monopolies and the few cases challenging mergers in the USA.
4. The criterion of ‘consumer welfare standard’ and the principle that antitrust law should serve consumer interests and that it should protect competition rather than individual competitors was an antitrust law introduced by, and named after, the 'Chicago school'.
The passage given below is followed by four alternate summaries. Choose the option that best captures the essence of the passage.
The dominant hypotheses in modern science believe that language evolved to allow humans to exchange factual information about the physical world. But an alternative view is that language evolved, in modern humans at least, to facilitate social bonding. It increased our ancestors’ chances of survival by enabling them to hunt more successfully or to cooperate more extensively. Language meant that things could be explained and that plans and past experiences could be shared efficiently.
The four sentences (labelled 1, 2, 3, 4) below, when properly sequenced would yield a coherent paragraph. Decide on the proper sequencing of the order of the sentences and key in the sequence of the four numbers as your answer:
1. Complex computational elements of the CNS are organized according to a “nested” hierarchic criterion; the organization is not permanent and can change dynamically from moment to moment as they carry out a computational task.
2. Echolocation in bats exemplifies adaptation produced by natural selection; a function not produced by natural selection for its current use is exaptation --feathers might have originally arisen in the context of selection for insulation.
3. From a structural standpoint, consistent with exaptation, the living organism is organized as a complex of “Russian Matryoshka Dolls” -- smaller structures are contained within larger ones in multiple layers.
4. The exaptation concept, and the Russian-doll organization concept of living beings deduced from studies on evolution of the various apparatuses in mammals, can be applied for the most complex human organ: the central nervous system (CNS).
The passage given below is followed by four alternate summaries. Choose the option that best captures the essence of the passage.
Aesthetic political representation urges us to realize that ‘the representative has autonomy with regard to the people represented’ but autonomy then is not an excuse to abandon one’s responsibility. Aesthetic autonomy requires cultivation of ‘disinterestedness’ on the part of actors which is not indifference. To have disinterestedness, that is, to have comportment towards the beautiful that is devoid of all ulterior references to use – requires a kind of aesthetic commitment; it is the liberation of ourselves for the release of what has proper worth only in itself.
Five jumbled up sentences, related to a topic, are given below. Four of them can be put together to form a coherent paragraph. Identify the odd one out and key in the number of the sentence as your answer:
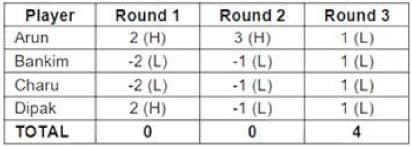
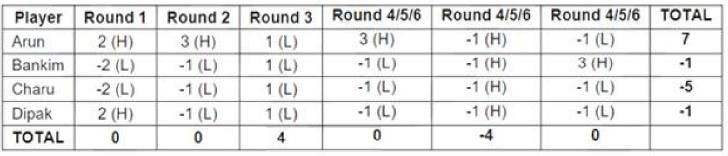
What were the bids by Arun, Bankim, Charu and Dipak, respectively in the first round?
In how many rounds did all four players make identical bids?