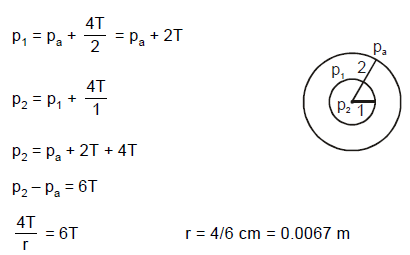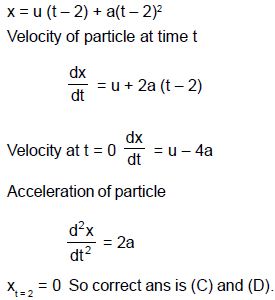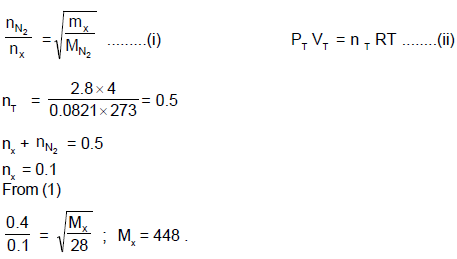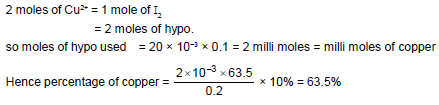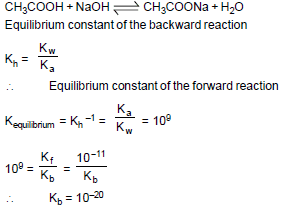JEE Advanced Test- 7 - JEE MCQ
30 Questions MCQ Test - JEE Advanced Test- 7
The spring block system lies on a smooth horizontal surface. The free end of the light spring is being pulled towards right with constant speed v0 = 2m/s. At t = 0 sec, the spring of spring constant k = 100 N/cm is unstretched and the block has a speed 1 m/s to left. The maximum
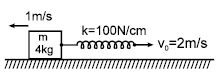
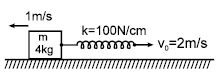
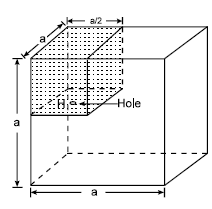
The figure shows a hollow cube of side 'a' of volume V. There is a small chamber of volume V/4 in the cube as shown. This chamber is completely filled by m kg of water. Water leaks through a hole H. Then the work done by gravity in this process assuming that the complete water finally lies at the bottom of the cube is :

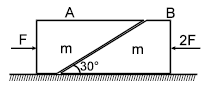
Two blocks ‘A’ and ‘B’ each of mass ‘m’ are placed on a smooth horizontal surface. Two horizontal force F and 2F are applied on the two blocks ‘A’ and ‘B’ respectively as shown in figure. The block A does not slide on block B. Then the normal reaction acting between the two blocks is :

A coin is released inside a lift at a height of 2 m from the floor of the lift. The height of the lift is 10 m. The lift is moving with an acceleration of 11 m/s2 downwards. The time after which the coin will strike the lift is :
The extension in a uniform rod of length l, mass m, cross section radius r and young’s modulus Y when it is suspended at one of its end is :
A spherical soap bubble of radius 1.0 cm is formed inside another of radius 2 cm. If a single soap bubble is formed which maintains the same pressure difference as inside the smaller and outside the larger bubble, the radius of this bubble is -
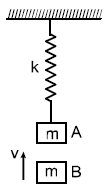
Block ‘ A ‘ is hanging from a vertical spring and is at rest. Block ‘ B ‘ strikes the block ‘A’ with velocity ‘ v ‘ and sticks to it. Then the value of ‘ v ‘ for which the spring just attains natural length is :
A small uniform tube is bent into a circular tube of radius R and kept in the vertical plane. Equal volumes of two liquids of densities ρ and σ (ρ > σ) fill half of the tube as shown. θ is the angle which the radius passing through the interface makes with the vertical.

A ball tied to the end of a string swings in a vertical circle under the influence of gravity
A particle moves along the X-axis as
x = u(t – 2) + a(t – 2)2
Statment–1 : Steady flow can be maintained in compressible liquids.
Statment–2 : Steady flow means all physical parameters related to the flow being constant with time though they may vary with position.
Statment–1 : In a circular motion, the force must be directed perpendicular to the velocity all the time.
Statment–2 : A centripetal force is required to provide the centripetal acceleration in a circular motion.
Statment–1 : The centre of gravity and centre of mass of a body may be at different positions.
Statment–2 : If the mass is uniformly distributed then only the centre of mass and centre of gravity of a body will be at the same place.
Statment-1 : Consider an object that floats in water but sinks in oil. When the object floats in water, half of it is submerged. If we slowly pour oil on top of water till it completely covers the object, the object moves up.
Statment-2 :As the oil is poured in the situation of statement-1, pressure inside the water will increase everywhere resulting in an increase in upward force on the object.
Consider a star and two planet system. The star has mass M. The planets A and B have the same mass m, radius a and they revolve around the star in circular orbits of radius r and 4r respectively (M > > m, r > > a). Planet A has intelligent life and the people of this planet have achieved a very high degree of technological advance. They wish to shift a geostationary satellite of their own planet to a geostationary orbit of planet B. They achieve this through a series of high precision maneuvers in which the satellite never has to apply brakes and not a single joule of energy is wasted. S1 is a geostationary satellite of planet A and S2 is a geostationary satellite of planet B. Neglect interaction between A and B, S1 and S2, S1 and B & S2 and A.
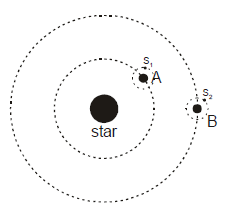
Q. If the time period of the satellite in geostationary orbit of planet A is T, then its time period in geostationary orbit of planet B is :
Consider a star and two planet system. The star has mass M. The planets A and B have the same mass m, radius a and they revolve around the star in circular orbits of radius r and 4r respectively (M > > m, r > > a). Planet A has intelligent life and the people of this planet have achieved a very high degree of technological advance. They wish to shift a geostationary satellite of their own planet to a geostationary orbit of planet B. They achieve this through a series of high precision maneuvers in which the satellite never has to apply brakes and not a single joule of energy is wasted. S1 is a geostationary satellite of planet A and S2 is a geostationary satellite of planet B. Neglect interaction between A and B, S1 and S2, S1 and B & S2 and A.

Q. If the radius of the geostationary orbit in planet A is given by then the time in which the geostationary satellite will complete 1 revolution is
I. 1 planet year = time in which planet revolves around the star
II. 1 planet day = time in which planet revolves about its axis.
Consider a star and two planet system. The star has mass M. The planets A and B have the same mass m, radius a and they revolve around the star in circular orbits of radius r and 4r respectively (M > > m, r > > a). Planet A has intelligent life and the people of this planet have achieved a very high degree of technological advance. They wish to shift a geostationary satellite of their own planet to a geostationary orbit of planet B. They achieve this through a series of high precision maneuvers in which the satellite never has to apply brakes and not a single joule of energy is wasted. S1 is a geostationary satellite of planet A and S2 is a geostationary satellite of planet B. Neglect interaction between A and B, S1 and S2, S1 and B & S2 and A.

Q. If planet A and B, both complete one revolution about their own axis in the same time, then the energy needed to transfer the satellite of mass m0 from planet A to planet B is -
In the figure the variation of potential energy of a particle of mass m = 2kg is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis.
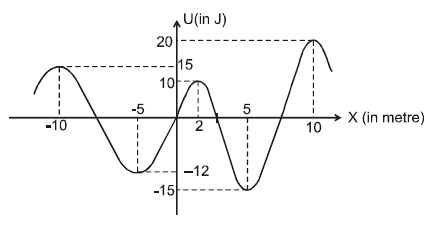
Q. If the particle is released at the origin then :
In the figure the variation of potential energy of a particle of mass m = 2kg is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis.

Q. If the particle is released at x = 2 + Δ where Δ → 0 (it is positive) then its maximum speed in subsequent motion will be :
In the figure the variation of potential energy of a particle of mass m = 2kg is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis.

Q. x = – 5 m and x = 10 m positions of the particle are respectively of
A particle is taken to a distance r (> R) from centre of the earth. R is radius of the earth. It is given velocity V which is perpendicular to . With the given values of V in column I you have to match the values of total energy and path of particle in column II. Here 'G' is the gravitational constant and 'M' is the mass of the earth.

An arrangement of the pipes is shown in the figure. The flow of water (incompressible and nonviscous) through the pipes is steady in nature. Three sections of the pipe are marked in which section 1 and section 2 are at same horizontal level, while being at a greater height than section 3. Correctly match order of the different physical parameter with the options given.
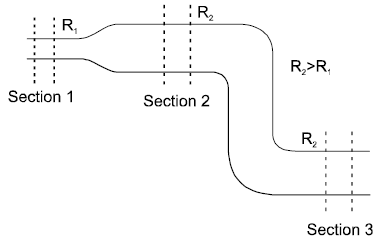
Column I Column II
(A) volume flow rate (p) same everywhere
(B) kinetic energy per unit mass (q) same at 2 and 3
(C) pressure in the sections. (r) maximum at 1
(D) flow speed in sections (s) minimum at 1
(t) maximum at 3
For 10 minute each, at 0 ºC, from two identical holes nitrogen and an unknown gas are leaked into a common vessel of 4 litre capacity. The resulting pressure is 2.8 atm and the mixture contains 0.4 mole of nitrogen. What is the molar mass of unknown gas?
A 0.200 gm sample containing copper (II) was analysed iodometrically, copper (II) is reduced to
copper (I) by iodine. 2Cu2+ + 4I– ——? 2 CuI + I2
If 20.0mL of 0.10 M Na2S2O3 is required for titration of the liberated iodine then the percentage of copper in the sample will be (Cu = 63.5 g/mole)
An ideal gaseous sample at initial state i (P0 , V0,T0) is allowed to expand to volume 2V0 using two different process; in the first process the equation of process is PV2 = K1 and in second process the equation of the process is PV = K2. Then
Given that T=298K
Now on the basis of above data which of the following predictions will be most appropriate under the standard conditions and reversible reaction.
An acid HA (Ka = 10–5) reacts with NaOH at 298 K. What would be the value of the rate constant of the reverse reaction at the same temperature if the rate constant of the forward reaction is 10–11 mol–1 L sec–1 ?
In a sample of H-atom electrons make transition from 5th excited state to ground state, producing all possible types of photons, then number of lines in infrared region are