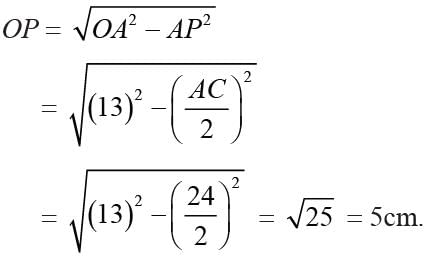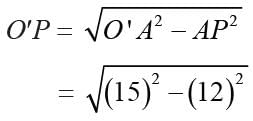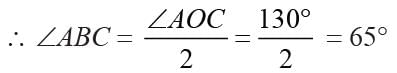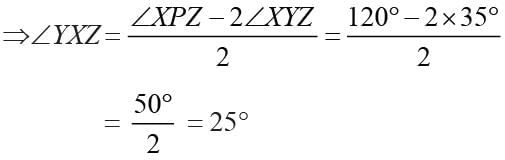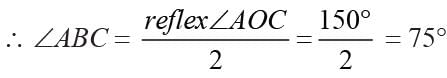Math Olympiad Test: Circles- 1 - Class 9 MCQ
10 Questions MCQ Test - Math Olympiad Test: Circles- 1
AB and CD are two parallel chords of a circle such that AB = 8 cm, and CD = 6cm. If the chords are on the opposite sides of the center and the distance between them is 7cm, then the diameter of the circle is:
Two circles of radii 13cm and 15cm intersect and the length of the common chord is 24 cm, then the distance between their centers is:
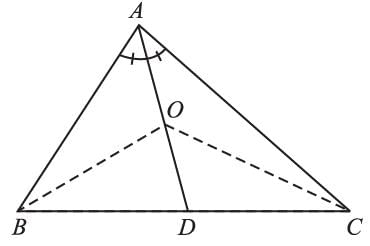
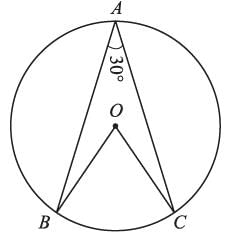
Bisector AD of ∠BAC of ∆ABC passes through the center of the circumcircle of ∆ABC, then,
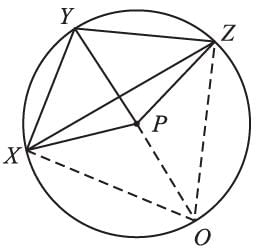
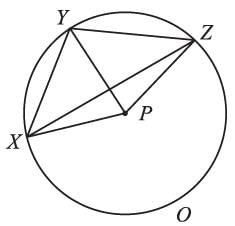
P is the center of the circle, and ∠XPZ = 120°, ∠XZY = 35°, then the measure of ∠YXZ is:
PQRS is a cyclic quadrilateral such that PR is the diameter of the circle. If ∠QPR = 64° and ∠SPR = 31°, then, ∠R =?
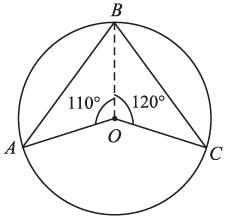
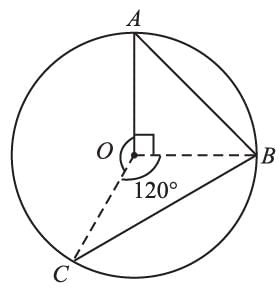
If A, B, C are three points on a circle with center O such that ∠AOB = 90° and ∠BOC = 120°, then ∠ABC =?
O is the center of the circle, with AC = 30 cm and DA = 10√5 cm, then the measure of DC is