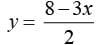Math Olympiad Test: Linear Educations in Two Variables- 2 - Class 9 MCQ
15 Questions MCQ Test - Math Olympiad Test: Linear Educations in Two Variables- 2
Which of the following are the solutions of the equation 2x + 3y = 13?
If 2x + 16y = 13 and x + y = p, have same set of solution, then the possible value of p is (are):
If x = k2 and y = k are solutions of equation x - 5y = -6 then k =?
The solution of equation x - y + 8 = 0 is x = k3 and y = 0, then k =?
If the equation (x + 3y) - (3x + y) + (x - y) = (α - b), then which of the following is a solution of the above equation?
The point of intersection of graphs of the equations 3x + 4y = 12 and 6x + 8y = 48 is
The point of intersection of 3x + 4y = 15 and x-axis will be
The graph of the equation 15x + 36y = 108 will cut the y- axis at:
The distance between the graphs of the equations x = 3 and x = -3 is
The equation 3x + 2y = 8 has
The equation of the parallel to x-axis and passing through the point (3, -4) will be:
The equation 3x = 9 is pitied on graph paper, then which point lies on the graph?
The monthly incomes of A and B are in the ratio 8 : 7 and their expedites are in the ratio 19 : 16 If the savings of both A and B is Rs. 2500, then the month income of A is
A man’s age is 3 times the sum of the ages of his 2 sons after 5 years, His age will be twice the sum of ages of his 2 sons. The age of man (in years) will be:
In a ΔABC, ∠C = 3, ∠B = 2(∠A + ∠B), then ∠C =?