Math Olympiad Test: Real Numbers- 1 - Class 10 MCQ
10 Questions MCQ Test - Math Olympiad Test: Real Numbers- 1
What is the L.C.M. of 144, 180 and 192 by prime factorization method?
What is the largest number that divides 445, 572 and 699 having remainders 4, 5, 6 respectively?
What is the largest positive integer that will divide 398, 436 and 542 leaving remainder 7, 11 and 15 respectively?
What is the largest number which divides 615 and 963 leaving remainder 6 in each case?
What is the smallest number that when divided by 35, 56, and 91 leaves remainder 7 in each case?
If the H.C.F. of 408 and 1032 is expressed in the form of 1032m - 408 × 5. What is the value of m?
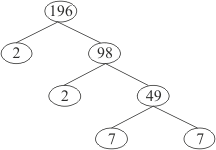
Find the sum of the exponents of the prime factors in the prime factorization of 196.
If 5005 is expressed in the term of product of price factors, then which prime factor is the largest?
The H.C.F of two numbers is 145, their L.C.M. is 2175. If one number is 725, then what is the other number?
If n is any natural number then 6n - 5n always ends with