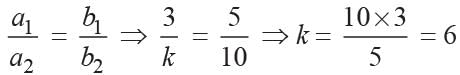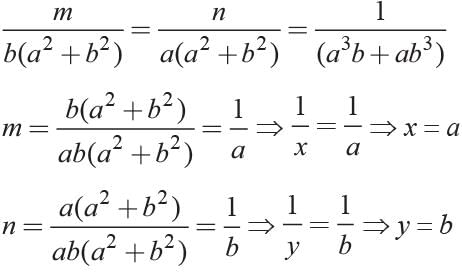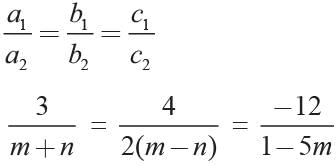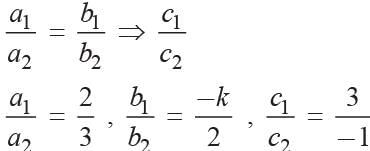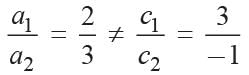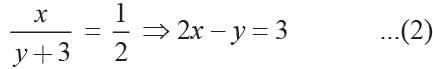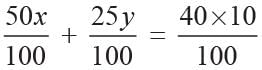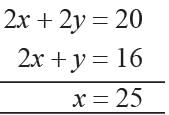Math Olympiad Test: Linear Equations in Two Variables- 2 - Class 10 MCQ
15 Questions MCQ Test - Math Olympiad Test: Linear Equations in Two Variables- 2
The sum of the digits of a two digits number is 12. The number obtained by interchanging the digits exceeds the given number by 18. What is that number?
Five years ago, Ram was thrice as old as Mohan. Ten years later Ram shall be twice as old as Mohan. What is the present age of Ram and Mohan?
What is the value of k for which the system of equations 3x + 5y = 0 and kx + 10y = 0, has a non-zero solution?
What are the values of x and y, if
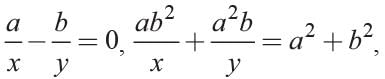
where x ≠ 0, y ≠ 0?
What are the values of m and n for which the system of linear equations has infinitely many solutions, 3x + 4y = 12, (m + n)x + 2(m - n)y = (5m - 1)?
What are the values of x and y if x + y = a + b, ax - by = a2 - b2?
What is the value of K for which the system has no solution?
2x - ky + 3 = 0; 3x + 2y - 1 = 0
The sum of the numerator and denominator of a fraction is 12. If the denominator is increased by 3, the fraction becomes 1/2. What is the fraction?
The larger of the two supplementary angles exceeds the smaller by 18º. What is the value of a larger angle?
A railway half ticket cost half the full fare and the reservation charge is the same on a half ticket as on a full ticket. one reserved first-class ticket from Delhi to Patna costs ₹ 216. One full and one half reserved first-class ticket cost ₹ 328. What is the reservation charge?
The student of a class are made to stand in rows. If 4 students are extra in each row, there would be 2 rows less. If 4 students are less to each row, there would be 4 rows more. What is the number of students in the class?
If three times the larger of two numbers is divided by the smaller one, we get 4 as quotient and 3 as remainder. If seven times the smaller number is divided by the larger one, we get 5 as the quotient and 1 as the remainder. What is the smaller number?
A chemist has one solution containing 50% acid and a second one containing 25% acid. How much of each should be used respectively to make 10 litres of a 40% acid solution?
A three digit number abc is 459 more than the sum of its digits. What is the sum of the 2 digit number ab and the 1-digit number a?
Swathi starts her job with a certain monthly salary and earns a fixed increment every year. If her salary was ₹ 22500 per month after 6 years of service and ₹ 30000 per month after 11 years of service. Find her salary in rupees after 8 years of service.