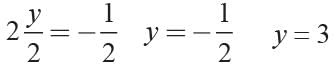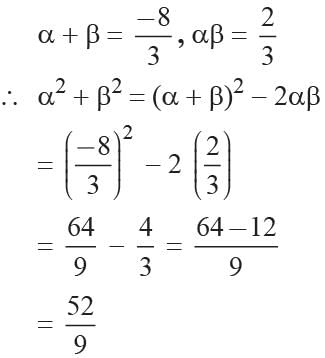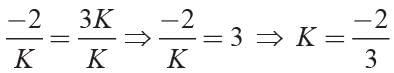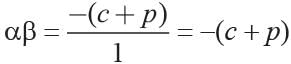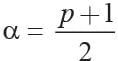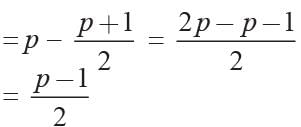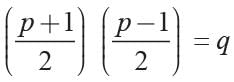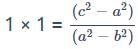Math Olympiad Test: Quadratic Equations- 2 - Class 10 MCQ
15 Questions MCQ Test - Math Olympiad Test: Quadratic Equations- 2
Find the value of x. (Be sure to give all solutions)
x2 - 6 = 138
x2 - 6 = 138
Find the values for x for the following equation.
x2 + 4x - 32 = 0
x2 + 4x - 32 = 0
Find the values of y for the following equation:
2y2 - 5y + 2 = 5
2y2 - 5y + 2 = 5
A ball is shot from a cannon into the air with an upward velocity of 36 ft/sec. The equation that gives the height (h) of the ball at any time (t) is: h(t) = -16t2 + 36t + 1.5. Find the maximum height attained by the ball.
If a < 0, then function f(x) = ax2 + bx + c has a maximum value at
If α and β are the roots of 3x2 + 8x +2 = 0 then what is the value α2 + β2?
If the sum of roots of the equation Kx2 + 2x + 3K = 0 is equal to their product, then the value of K is
The roots of a quadratic equation are 7 and -3, then what is the equation?
If one root of the equation x2 + px + 12 = 0 is 4, while the equation x2 + px + q = 0 has equal roots then the value of q is
If α , β are the roots of the equation x2 - p (x + 1) - c = 0 then (α + 1) (β + 1) is equal to
If the difference of the root x2 -px + q = 0 is unity then
If a, b are the roots of the equation x2 + x + 1 = 0 then a2 + b2 = ?
If A and B are the roots of the quadratic equation x2 - 12x + 27 = 0, then A3 + B3 is
If the quadratic equation (a2 - b2)x2 + (b2 - c2)x + (c2 - a2) = 0 has equal roots, then which of the following is true?