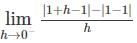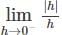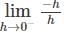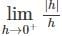Mathematics: CUET Mock Test - 2 - Commerce MCQ
30 Questions MCQ Test - Mathematics: CUET Mock Test - 2
A particle moves in a straight-line OA; the distance of the particle from O at time t seconds is x ft, where x = a + bt + ct2 (a, b > 0). What will be the nature of motion of the particle when c = 0?
A pipe can empty (5/6)th part of a cistern in 20 minutes. The part of cistern which will be empty in 9 minutes is:
The system of linear inequalities 2x − 1 ≥ 3 and x − 3 > 5 has solution:
The values of x which statisfied |3x| ≥ |6 − 3x|
A. (0, 1]
B. [1, 4]
C. (4, ∞)
D. (−1, 0)
E. (−∞, 0)
Choose the correct answer from the options given below:
If  is skew symmetric matrix, then value of x2 + y2 + z2 + u2 + v2 + w2 is:
is skew symmetric matrix, then value of x2 + y2 + z2 + u2 + v2 + w2 is:
Let A = 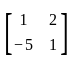 and A-1 = xA + yI, then value of x and y are
and A-1 = xA + yI, then value of x and y are
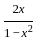 ) with respect to sin-1(
) with respect to sin-1(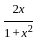 ) is equal to
) is equal to
A particle moving in a straight line traverses a distance x in time t. If t = x2/2 + x, then which one is correct?
A particle moves with uniform acceleration along a straight line and describes distances 21m, 43m and 91m at times 2, 4 and 7 seconds, respectively.What is the velocity of the particle in 3 seconds?
The distance x of a particle moving along a straight line from a fixed point on the line at time t after start is given by t = ax2 + bx + c (a, b, c are positive constants). If v be the velocity of the particle and u(≠0) be the initial velocity of the particle then which one is correct?
A particle moves in a straight line and its velocity v at time t seconds is given byv = 3t2 – 4t + 5 cm/second. What will be the distance travelled by the particle during first 3 seconds after the start?
A particle moves with uniform acceleration along a straight line and describes distances 21m, 43m and 91m at times 2, 4 and 7 seconds,respectively.What is the distance described by the particle in 3 seconds?
A particle moves in a horizontal straight line under retardation kv3, where v is the velocity at time t and k is a positive constant. If initial velocity be u and x be the displacement at time,then which one is correct?
The distance s of a particle moving along a straight line from a fixed-pointO on the line at time t seconds after start is given by x = (t – 1)2(t – 2)2. What will be the distance of the particle from O when its velocity is zero?
What will be the nature of the equation sin(x + α)/sin(x + β)?
Given, f(x) = x3 – 12x2 + 45x + 8. What is the maximum value of f(x)?
Given, f(x) = x3 – 12x2 + 45x + 8. What is the minimum value of f(x)?
A particle is moving in a straight line and its distance x from a fixed point on the line at any time t seconds is given by, x = t4/12 – 2t3/3 + 3t2/2 + t + 15. At what time is the velocity minimum?
Given, f(x) = x3 – 12x2 + 45x + 8. At which point does f(x) has its maximum?
Given, f(x) = x3 – 12x2 + 45x + 8. At which point does f(x) has its minimum?
At which point does f(x) = |x – 1| has itslocal minimum?
A particle is moving in a straight line and its distance x from a fixed point on the line at any time t seconds is given by, x = t4/12 – 2t3/3 + 3t2/2 + t + 15. What is the minimum velocity?
What will be the equation of the normal to the parabola y2 = 5x that makes an angle 45° with the x axis?
What will be the equation of the normal to the parabola y2 = 3x which is perpendicular to the line y = 2x + 4?
What will be the length of a tangent from the point (7, 2) to the circle 2x2 + 2y2 + 5 x + y = 15?
What will be the equation of the circle which touches the line x + 2y + 5 = 0 and passes through the point of intersection of the circle x2 + y2 = 1 and x2 + y2 + 2x + 4y + 1 = 0?



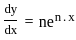 .... (1)
.... (1)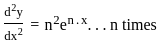
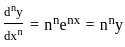
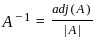 where adj(A) is called an adjoint matrix.
where adj(A) is called an adjoint matrix.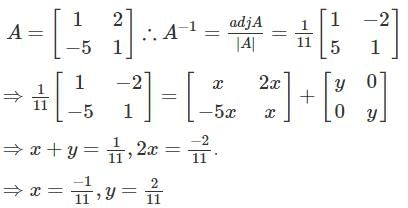
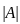
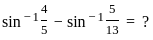
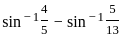
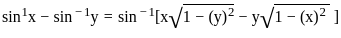
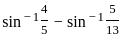
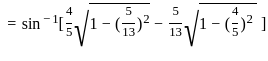
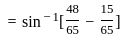
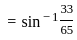
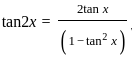
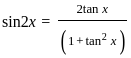
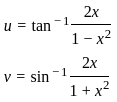
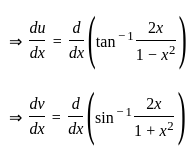
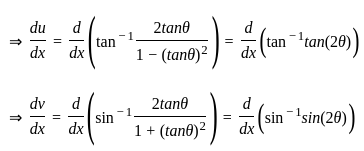
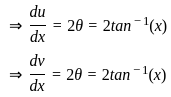
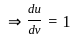
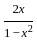
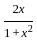
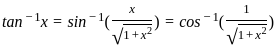
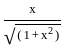 )
)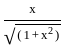 , since sin(sin
, since sin(sin − hf(c + h) – f(c)
− hf(c + h) – f(c)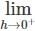 + hf(c + h) – f(c) are finite and equal.
+ hf(c + h) – f(c) are finite and equal.