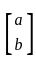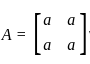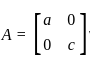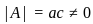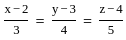Mathematics: CUET Mock Test - 4 - Commerce MCQ
30 Questions MCQ Test - Mathematics: CUET Mock Test - 4
Which one of the following is correct if we differentiate the equation xy = aex + be-x two times?
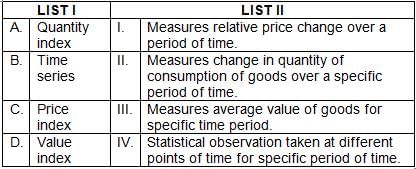
Match List I with List II
Choose the correct answer from the options given below:

Given that ∑p0q0 = 700, ∑p0q1 = 1450, ∑p1q0 = 855 and ∑p1q1 = 1300. Where subscripts 0 and 1 are used for the base year and a current year respectively. The Laspeyer's price index number is:
If y = a + b(x − 2005) fits the time series data:
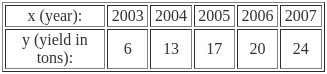
Then the value of a + b is:
Which of the following statements are correct?
A. If discount rate > coupon rate, then present value of a bond > face value
B. An annuity in which the periodic payment begins on a fixed date and contimues forever is called perpetuity
C. The issuer of bond pays interest at fixed interval at fixed rate of interest to investor is called coupon payment
D. A sinking fund is a fixed payment made by a borrower to a lender at a specific date every month to clear off the loan
E. The issues of bond repays the principle i.e. face value of the bond to the investor at a later date termed as maturity date
Choose the correct answer from the options given below:
Which of the following statements is true?
A. EMI in flat rate method, EMI = 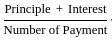
B. EMI in reducing balance method, EMI = P × 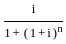 where P = Principle. i = interest rate, n = no. of payments
where P = Principle. i = interest rate, n = no. of payments
C. In sinking fund, a fixed amount at regular intervals is deposited.
D. Approximate Yield to Maturity = 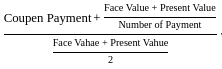
Choose the correct answer from the options given below:
The area in the first quadrant between x2 + y2 = π2 and y = sin x is,
Area bounded by the curves y = x sin x and X-axis between x = 0 and x = 2π is
The angle between two planes 3x – 6y + 2z = 7 and 2x + 2y – 2z = 5 is
Let A be a 2 × 2 symmetric matrix with integer entries. Then A is invertible if
1. the first column of A is the transpose of the second row of A
2. the second row of A is the transpose of first column of A
3. A is a diagonal matrix with nonzero entries in the main diagonal
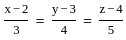 ?
?
What is the differential equation of all parabolas whose directrices are parallel to the x-axis?
What will be the required solution of d2y/dx2 – 3dy/dx + 4y = 0?
What is the solution of the given equation (D + 1)2y = 0 given y = 2 loge 2 when x = loge 2 and y = (4/3) loge3 when x = loge3?
If, A and B are arbitrary constants then what will be the differential equation of y = Ax + B/x?
What will be the value of C if C the constant of the coefficient of the solution of the given equation (D + 1)2y = 0 given y = 2 loge 2 when x = loge 2 and y = (4/3) loge3 when x = loge3?
What is thedifferential equation whose solution represents the family y = ae3x + bex?
If y = t(x) be a differentiable function ᵾ x € R, then which of the following is always true?
What will be the general solution of the differential equation d2y/dx2 = e2x(12 cos3x – 5 sin3x)? (here, A and B are integration constant)
Which of the following is the valid differential equation x = a cos(αt + β)?
If, A normal is drawn at a point P(x, y) of a curve. It meets the x-axis at Q. If PQ is of constant length k. What kind of curve is passing through (0, k)?
What is the solution of (y(dy/dx) + 2x)2 = (y2 + 2x2)[1 + (dy/dx)2]?
A particle starts from the origin with a velocity 5cm/sec and moves in a straight line, its acceleration at time t seconds being (3t2 – 5t)cm/sec2. What will be the velocity of the particle?
What will be the differential equation form of √(a2 + x2)dy/dx + y = √(a2 + x2) – x?
A curve passes through (1, 1) such that the triangle formed by the coordinate axes and the tangent at any point of the curve is in the first quadrant and has its area equal to 2. What will be the equation of the curve?
A curve passes through (1, 1) such that the triangle formed by the coordinate axes and the tangent at any point of the curve is in the first quadrant and has its area equal to 2. What is the differential equation?
What will be the value of dy/dx – a/x * y = (x + 1)/x?
What is the solution of dy/dx = (6x + 9y – 7)/(2x + 3y – 6)?
A particle starts from the origin with a velocity 5cm/sec and moves in a straight line, its acceleration at time t seconds being (3t2 – 5t)cm/sec2. What will be the distance from the origin at the end of 4 seconds?
What is the equation of the curve passing through (1, 0) of (y(dy/dx) + 2x)2 = (y2 + 2x2)[1 + (dy/dx)2]?



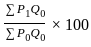 =
= 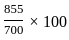
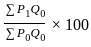
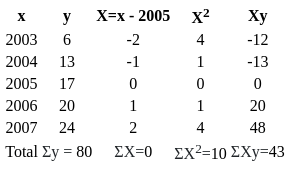
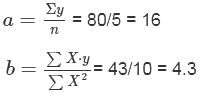
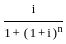 , where P = Principal loan amount, r = monthly interest rate, n = number of monthly installments.
, where P = Principal loan amount, r = monthly interest rate, n = number of monthly installments.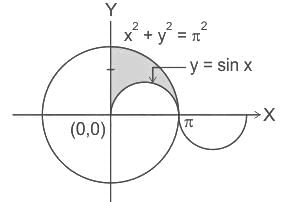
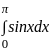
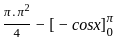
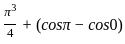
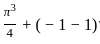
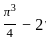
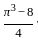 sq. units
sq. units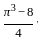 sq. units.
sq. units.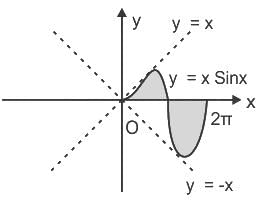
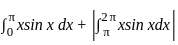
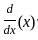 ∫ sin x dx)dx]π2π|
∫ sin x dx)dx]π2π|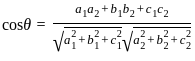
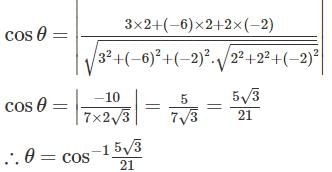
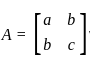
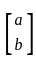 and
and 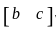 are transpose
are transpose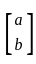 =
= 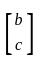
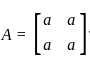
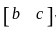 and
and 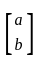 and are transpose
and are transpose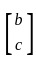 =
=