All Courses
Get the App Signup / Login
Sign in Open App
CAT Exam  >  CAT Tests  >  Test Level 1: Binary Logic - CAT MCQ

Test Level 1: Binary Logic - CAT MCQ


Test Description

15 Questions MCQ Test - Test Level 1: Binary Logic

Test Level 1: Binary Logic for CAT 2024 is part of CAT preparation. The Test Level 1: Binary Logic questions and answers have been prepared according to the CAT exam syllabus.The Test Level 1: Binary Logic MCQs are made for CAT 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test Level 1: Binary Logic below.
Solutions of Test Level 1: Binary Logic questions in English are available as part of our course for CAT & Test Level 1: Binary Logic solutions in Hindi for CAT course. Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free. Attempt Test Level 1: Binary Logic | 15 questions in 30 minutes | Mock test for CAT preparation | Free important questions MCQ to study for CAT Exam | Download free PDF with solutions
Test Level 1: Binary Logic - Question 1
Save

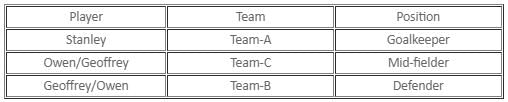
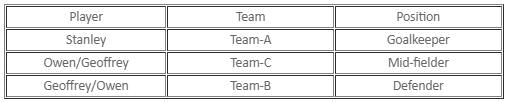
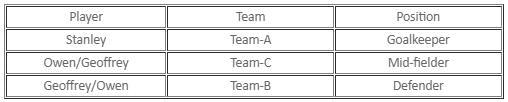
Three persons Bryan, Edward and Avril, each of whom is of a different community, are standing together. When asked about their community, Bryan replied, "I am a Gitty. Avril is Amora.". Then Edward belongs to which community?

Detailed Solution for Test Level 1: Binary Logic - Question 1

In the given statement, Bryan said that he was a Gitty. No truth-teller or liar can make a statement that he is a Gitty (always a lie). Bryan must be an alternator, that is, a Pixie; and his first statement is a lie. Hence, his second statement is true; Avril is an Amora. Edward is a Gitty.

Test Level 1: Binary Logic - Question 2
Save

Each of three different persons Mary, Helen and Patricia belong to a different community. In the conversation, Patricia said, "I am a Pixie. Mary is not a Gitty.'' Who among the three persons is an Amora?

Detailed Solution for Test Level 1: Binary Logic - Question 2

From the given statement, Patricia cannot be an Amora. He cannot be a Gitty, as if he is a Gitty, his second statement will be true, which is a contradiction. Hence, Patricia must be a Pixie and Mary is a Gitty. Helen is an Amora.

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test Level 1: Binary Logic - Question 3
Save

If Bruce is not a Pixie, then who among the three persons is the Gitty?

Detailed Solution for Test Level 1: Binary Logic - Question 3

Case 1: Assuming Hamish to be Amora
Hamish:
I am an Amora. ---TRUE
Bruce is an Amora. --TRUE
This is a contradiction, as 2 people cannot be from the same community.
Case 2: Assuming Hamish to be Gitty
I am an Amora. ---FALSE
Bruce is an Amora. --FALSE
This means Bruce must be from Pixie, since Bruce is not from Amora and Hamish is already assumed to belong to Gitty.
But the question says that Bruce is not from Pixie. Hence, this case is also disregarded .
Case 3: Assuming Hamish to be Pixie
I am an Amora. ---FALSE
Bruce is an Amora. --TRUE
Thus, Bruce is an Amora, Hamish is Pixie, and Colin is Gitty.
Case 4: Assuming Hamish to be Pixie
I am an Amora. ---TRUE
Bruce is an Amora. --FALSE
This is not possible since then Hamish would again belong to both Pixie and Amora.
Thus, only Case 3 is valid.

Test Level 1: Binary Logic - Question 4
Save

Who among the three must have stolen Antique Gun?
Detailed Solution for Test Level 1: Binary Logic - Question 4

(i) Assuming that Thief-1 always speaks the truth:

(ii) Assuming that Thief-2 always speaks the truth:

(iii) Assuming that Thief-3 always speaks the truth:

From case (i), we can conclude that Thief-3 stole Antique Gun.

Test Level 1: Binary Logic - Question 5
Save

Which item did Thief-2 steal?
Detailed Solution for Test Level 1: Binary Logic - Question 5

The only posisble scenario is :
Case 2:
Thief-1:
I stole Bronze Statue. TRUE
Thief-2 stole Rare Painting. TRUE
Thief-2:
I stole Bronze Statue. FALSE
Thief-3 stole Antique Gun. TRUE
Thief-3:
Thief-1 stole Rare Painting. FALSE
Thief-2 stole Bronze Statue. FALSE
Hence, ans is 3.

Test Level 1: Binary Logic - Question 6
Save

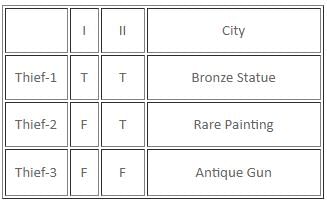
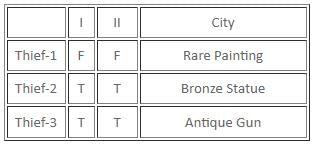
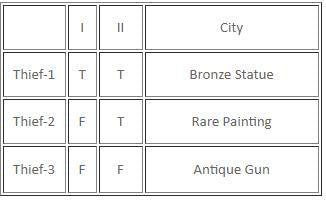
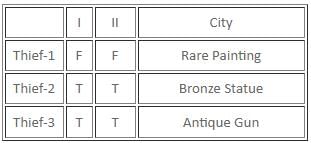
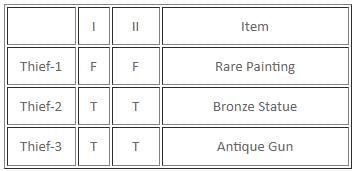
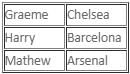
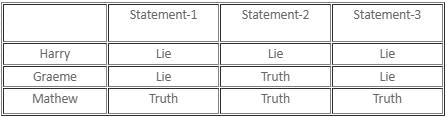
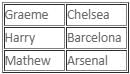
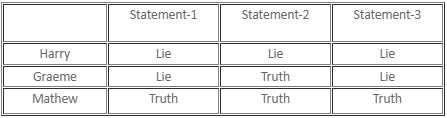
If there are exactly two thieves who always tell the truth and the third thief either always lies or alternates between the truth and a lie, then which of the following statements must be false?
Detailed Solution for Test Level 1: Binary Logic - Question 6

(i) Assuming that Thief-1 always speaks the truth:

(ii) Assuming that Thief-2 always speaks the truth:

(iii) Assuming that Thief-3 always speaks the truth:

'Thief-3 did not steal Antique Gun' must be a false statement.

Test Level 1: Binary Logic - Question 7
Save

Which team is the Defender playing for?
Detailed Solution for Test Level 1: Binary Logic - Question 7

It is given that every player spoke exactly two false statements, hence one true statement. Let the first statement of Stanley be true. Hence, the other two must be false. Therefore, Stanley is not playing for Team-A. Owen is not a Mid-fielder and Geoffrey is not playing for Team-C.
Owen's second statement is therefore true. Hence, his first and third statements must be false. Hence, Owen is not a Defender and Stanley is not a Mid-fielder. Owen has to be a Goalkeeper. Stanley should be a Defender. Geoffrey must be a Mid-fielder.
Hence, Geoffrey's last statement is true. But Geoffrey's first statement is also true. Since this is not possible, Stanley's first statement cannot be true.
Let the second statement of Stanley be true. Therefore, Owen is a Mid-fielder. From his other two statements, we can say that Stanley is from Team-A and Geoffrey is from Team-B. Hence, Owen is from Team-C. Owen's second statement is true. His first and third statements are false. Geoffrey's second statement is true. His first and third statements must be false. Therefore, Stanley must be a Goalkeeper and Geoffrey must be a Defender. This is one possible case.
Let Stanley's third statement be true. Geoffrey must be from Team-C. From his first statement, we get that Stanley must be from Team-A. Therefore, Owen must be from Team-B. Owen is not a Mid-fielder.
Owen's second statement and Geoffrey's second statement are false. The only case possible in which both Owen and Geoffrey tell one true statement each is when Owen's first statement and Geoffrey's third statement are true. Hence, Owen is a Defender, Geoffrey is a Mid-fielder and Stanley is a Goalkeeper. This is another possible case.
The possible cases are presented in the following table:

Test Level 1: Binary Logic - Question 8
Save

The player from Team-C plays at which position?
Detailed Solution for Test Level 1: Binary Logic - Question 8

Given that every player spoke exactly two false statements, hence they all spoke one true statement. Let the first statement of Stanley be true. Hence, the other two must be false. Therefore, Stanley is not playing for Team-A. Owen is not a mid-fielder and Geoffrey is not playing for Team-C.
Owen's second statement is, therefore, true. Hence, his first and third statements must be false, which means that Owen is not a defender and Stanley is not a mid-fielder. Owen has to be a goalkeeper. Stanley should be a defender. Geoffrey must be a mid-fielder.
Hence, Geoffrey's last statement is true. But Geoffrey's first statement is also true. Since this is not possible, Stanley's first statement cannot be true.
Let the second statement of Stanley be true. Therefore. Owen is a mid-fielder. From his other two statements, we can say that Stanley is from Team-A and Geoffrey is from the Team-B. Hence, Owen is from the Team-C. Owen's second statement is true. His first and third statements are false. Geoffrey's second statement is true. His first and third statements must be false. Therefore, Stanley must be a goalkeeper and Geoffrey must be a defender. This is one possible case.
Let Stanley's third statement be true. Geoffrey must be from Team-C. According to his first statement, Stanley must be from Team-A. Therefore, Owen must be from Team-B. Owen is not a mid-fielder.
Owen's second statement and Geoffrey's second statement are false. The only case possible in which both Owen and Geoffrey tell one true statement each is when Owen's first statement and Geoffrey's third statement are true. Hence, Owen is a defender, Geoffrey is a mid-fielder and Stanley is a goalkeeper. This is another possible case.

Test Level 1: Binary Logic - Question 9
Save

Which team is Owen from?
Detailed Solution for Test Level 1: Binary Logic - Question 9

Given that every player spoke exactly two false statements, hence they all spoke one true statement. Let the first statement of Stanley be true. Hence, the other two must be false. Therefore, Stanley is not playing for Team-A. Owen is not a mid-fielder and Geoffrey is not playing for Team-C.
Owen's second statement is, therefore, true. Hence, his first and third statements must be false, which means that Owen is not a defender and Stanley is not a mid-fielder. Owen has to be a goalkeeper. Stanley should be a defender. Geoffrey must be a mid-fielder.
Hence, Geoffrey's last statement is true. But Geoffrey's first statement is also true. Since this is not possible, Stanley's first statement cannot be true.
Let the second statement of Stanley be true. Therefore. Owen is a mid-fielder. From his other two statements, we can say that Stanley is from Team-A and Geoffrey is from the Team-B. Hence, Owen is from the Team-C. Owen's second statement is true. His first and third statements are false. Geoffrey's second statement is true. His first and third statements must be false. Therefore, Stanley must be a goalkeeper and Geoffrey must be a defender. This is one possible case.
Let Stanley's third statement be true. Geoffrey must be from Team-C. According to his first statement, Stanley must be from Team-A. Therefore, Owen must be from Team-B. Owen is not a mid-fielder.
Owen's second statement and Geoffrey's second statement are false. The only case possible in which both Owen and Geoffrey tell one true statement each is when Owen's first statement and Geoffrey's third statement are true. Hence, Owen is a defender, Geoffrey is a mid-fielder and Stanley is a goalkeeper. This is another possible case.
The possible cases are presented in the following table:

Hence, Owen can be from Team-C or Team-B, which means that it cannot be determined.

Test Level 1: Binary Logic - Question 10
Save

Which of the following is true for the goalkeeper?
Detailed Solution for Test Level 1: Binary Logic - Question 10

Given that every player spoke exactly two false statements, hence they all spoke one true statement. Let the first statement of Stanley be true. Hence, the other two must be false. Therefore, Stanley is not playing for Team-A. Owen is not a mid-fielder and Geoffrey is not playing for Team-C.
Owen's second statement is, therefore, true. Hence, his first and third statements must be false, which means that Owen is not a defender and Stanley is not a mid-fielder. Owen has to be a goalkeeper. Stanley should be a defender. Geoffrey must be a mid-fielder.
Hence, Geoffrey's last statement is true. But Geoffrey's first statement is also true. Since this is not possible, Stanley's first statement cannot be true.
Let the second statement of Stanley be true. Therefore. Owen is a mid-fielder. From his other two statements, we can say that Stanley is from Team-A and Geoffrey is from the Team-B. Hence, Owen is from the Team-C. Owen's second statement is true. His first and third statements are false. Geoffrey's second statement is true. His first and third statements must be false. Therefore, Stanley must be a goalkeeper and Geoffrey must be a defender. This is one possible case.
Let Stanley's third statement be true. Geoffrey must be from Team-C. According to his first statement, Stanley must be from Team-A. Therefore, Owen must be from Team-B. Owen is not a mid-fielder.
Owen's second statement and Geoffrey's second statement are false. The only case possible in which both Owen and Geoffrey tell one true statement each is when Owen's first statement and Geoffrey's third statement are true. Hence, Owen is a defender, Geoffrey is a mid-fielder and Stanley is a goalkeeper. This is another possible case.
The possible cases are presented in the following table:

The name of the goalkeeper is Stanley.

Test Level 1: Binary Logic - Question 11
Save

Which of the following statements is/are definitely true?
Detailed Solution for Test Level 1: Binary Logic - Question 11

Given that every player spoke exactly two false statements, hence they all spoke one true statement. Let the first statement of Stanley be true. Hence, the other two must be false. Therefore, Stanley is not playing for Team-A. Owen is not a mid-fielder and Geoffrey is not playing for Team-C.
Owen's second statement is, therefore, true. Hence, his first and third statements must be false, which means that Owen is not a defender and Stanley is not a mid-fielder. Owen has to be a goalkeeper. Stanley should be a defender. Geoffrey must be a mid-fielder.
Hence, Geoffrey's last statement is true. But Geoffrey's first statement is also true. Since this is not possible, Stanley's first statement cannot be true.
Let the second statement of Stanley be true. Therefore. Owen is a mid-fielder. From his other two statements, we can say that Stanley is from Team-A and Geoffrey is from the Team-B. Hence, Owen is from the Team-C. Owen's second statement is true. His first and third statements are false. Geoffrey's second statement is true. His first and third statements must be false. Therefore, Stanley must be a goalkeeper and Geoffrey must be a defender. This is one possible case.
Let Stanley's third statement be true. Geoffrey must be from Team-C. According to his first statement, Stanley must be from Team-A. Therefore, Owen must be from Team-B. Owen is not a mid-fielder.
Owen's second statement and Geoffrey's second statement are false. The only case possible in which both Owen and Geoffrey tell one true statement each is when Owen's first statement and Geoffrey's third statement are true. Hence, Owen is a defender, Geoffrey is a mid-fielder and Stanley is a goalkeeper. This is another possible case.
The possible cases are presented in the following table:

Hence, all are true. 

Test Level 1: Binary Logic - Question 12
Save

The person who supports Barcelona is 
Detailed Solution for Test Level 1: Binary Logic - Question 12

After going through all statements made by Graeme, Harry, and Mathew, one can make out that Mathew's second statement is either a true statement of a truth-teller or a false statement of an alternator, irrespective of which Mathew's first and third statements have to be true. This gives us the following result:

Based on above, we can determine that Graeme's first statement is false and second one is true. As the three of them have to be either a truth-teller, a liar, or an alternator, we can conclude that Graeme is an alternator and her third statement is hence false (which means Mathew is not an alternator). This leads us to the conclusion that Mathew is a truth-teller. Thus, Mathew's second statement can also be marked as true.
Hereafter, when we analyse Harry's statements, we realise that they all are false; so Harry must be a liar. With 'T' standing for true and 'F' for false, the nature of the statements will be as follows:

Hence, Harry supports Barcelona.

Test Level 1: Binary Logic - Question 13
Save

Who among the following is a liar?
Detailed Solution for Test Level 1: Binary Logic - Question 13

After going through all statements made by Graeme, Harry, and Mathew, one can make out that Mathew's second statement is either a true statement of a truth-teller or a false statement of an alternator, irrespective of which Mathew's first and third statements have to be true. This gives us the following result:

Based on above, we can determine that Graeme's first statement is false and second one is true. As the three of them have to be either a truth-teller, a liar, or an alternator, we can conclude that Graeme is an alternator and her third statement is hence false (which means Mathew is not an alternator). This leads us to the conclusion that Mathew is a truth-teller. Thus, Mathew's second statement can also be marked as true.
Hereafter, when we analyse Harry's statements, we realise that they all are false; so Harry must be a liar. With 'T' standing for true and 'F' for false, the nature of the statements will be as follows:

Harry is a liar.

Test Level 1: Binary Logic - Question 14
Save

Which of the following statements is/are false?
Detailed Solution for Test Level 1: Binary Logic - Question 14

After going through all statements made by Graeme, Harry, and Mathew, one can make out that Mathew's second statement is either a true statement of a truth-teller or a false statement of an alternator, irrespective of which Mathew's first and third statements have to be true. This gives us the following result:

Based on above, we can determine that Graeme's first statement is false and second one is true. As the three of them have to be either a truth-teller, a liar, or an alternator, we can conclude that Graeme is an alternator and her third statement is hence false (which means Mathew is not an alternator). This leads us to the conclusion that Mathew is a truth-teller. Thus, Mathew's second statement can also be marked as true.
Hereafter, when we analyse Harry's statements, we realise that they all are false; so Harry must be a liar. With 'T' standing for true and 'F' for false, the nature of the statements will be as follows:
All the above statements are false.

Test Level 1: Binary Logic - Question 15
Save

Who among the following supports Arsenal?
Detailed Solution for Test Level 1: Binary Logic - Question 15

After going through all statements made by Graeme, Harry, and Mathew, one can make out that Mathew's second statement is either a true statement of a truth-teller or a false statement of an alternator, irrespective of which Mathew's first and third statements have to be true. This gives us the following result:

Based on above, we can determine that Graeme's first statement is false and second one is true. As the three of them have to be either a truth-teller, a liar, or an alternator, we can conclude that Graeme is an alternator and her third statement is hence false (which means Mathew is not an alternator). This leads us to the conclusion that Mathew is a truth-teller. Thus, Mathew's second statement can also be marked as true.
Hereafter, when we analyse Harry's statements, we realise that they all are false; so Harry must be a liar. With 'T' standing for true and 'F' for false, the nature of the statements will be as follows:

Hence, Mathew supports Arsenal.

Information about Test Level 1: Binary Logic Page
In this test you can find the Exam questions for Test Level 1: Binary Logic solved & explained in the simplest way possible. Besides giving Questions and answers for Test Level 1: Binary Logic, EduRev gives you an ample number of Online tests for practice

Top Courses for CAT

Download as PDF

Top Courses for CAT

Important Questions for Test Level 1: Binary Logic

Find all the important questions for Test Level 1: Binary Logic at EduRev.Get fully prepared for Test Level 1: Binary Logic with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Test Level 1: Binary Logic syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Test Level 1: Binary Logic resources.

Test Level 1: Binary Logic MCQs with Answers

Prepare for the Test Level 1: Binary Logic within the CAT exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Test Level 1: Binary Logic

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Test Level 1: Binary Logic with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup